广西南宁02-03年上学期高二数学期中考试
一、选择题(每小题只有一个正确答案,每小题3分,共36分)
1.不等式-3x2+x+2<0的解集为( )
A.(-![]() ,1) B.(-1,
,1) B.(-1,![]() ) C.(-∞,
) C.(-∞,![]() )∪(1,+∞)
)∪(1,+∞)
D.(-∞,-1)∪(![]() ,+∞)
,+∞)
2.过点A(0,2)、B(3,1)两点的直线的倾斜角为( )
A.arctg![]() B、arctg(-
B、arctg(-![]() ) C、π+arctg
) C、π+arctg![]() D、π-arctg
D、π-arctg![]()
3.一直线方程为ax+by+c=0,且ac>0,bc<0,则该直线必经过( )
A、第一、二、三象限 B、第一、二四象限
C、第二、三、四象限 D、第一、三、四象限
4.函数y=3x+![]() 的值域为(
)
的值域为(
)
A、![]() B、
B、![]()
C、![]() ∪
∪![]() D、前三项都不对
D、前三项都不对
5.△ABC中,A点坐标为(1,2),重心G点坐标为(0,0),则BC中点坐标为( )
A、(-![]() ,-1) B、(-1,-2) C、(
,-1) B、(-1,-2) C、(![]() ,1) D、条件不足,不能确定
,1) D、条件不足,不能确定
6.一直线在x轴、y轴上截距互为相反数,且过点(1,2),则该址线方程必为( )
A、y=2x B、x=2y C、y=x+1 D、前三项都不对
7.直线l1,l2,l3的倾斜角分别为α1,α2,α3,斜率分别为k1,k2,k3,若
k1<k2<0<k3,则α1,α2,α3的大小关系为( )
A、α1<α2<α3 B、α1>α2>α3
C、α2<α1<α3 D、α2>α1>α3
8.不等式(1-x)(x+2)2(x-3)<0的解集为( )
A、(-2,1)∪(3,+∞) B、(-∞,-2)∪(1,3)
C、(-∞,-2)∪(-2,1)∪(3,+∞) D、(-∞,1)∪(3,+∞)
9.若直线(m+1)x+(m+4)y-m=0与直线2x+(m+2)y+m=0平行,则m的值为( )
A、m=-3或m=2 B、m=-3 C、m=2 D、m=-3或m=0
10.一长方体的体积为V,则其表面积的最小值为( )
A、2V B、3V![]() C、3V
C、3V![]() D、6V
D、6V![]()
11.下列不等式中,成立的个数为( )
①a2+b2≥2ab; ②ab≤![]() ; ③
; ③![]()
④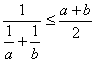 (a,b∈(0,+∞)
(a,b∈(0,+∞)
A、4 B、3 C、2 D、1
12.已知不等式a≥│x-1│-│x+3│对一切实数x都成立,则a的取值范围是( )
A、[ -4,+∞]) B、[ 4,+∞]) C、[ -4,4] D、[ 0,+∞])
二、填空题(每小题3分,共12分)
13.已知直线mx+ny=3m的系数m,n满足条件m+2n=4,则该直线必过定点 。
14.现有浓度为7%的食盐水2吨,需将它制成工业生产所需的浓度在5%到6%之间(不包括5%和6%)的食盐水,设需要加入浓度为4%的食盐水x吨,则x的取值范围为 。
15.不等式![]() <1的解集为(-∞,1)∪(2,+∞),则a的值等于
。
<1的解集为(-∞,1)∪(2,+∞),则a的值等于
。
16.不等式![]() <x+1的解集为
。
<x+1的解集为
。
三、解答题(共6小题,共52分)
17.(8分)解不等式log![]()
![]() ≥1
≥1
18.(8分)已知a、b、c是不全相等的正数,求证:![]() <a+b+c
<a+b+c
19.(8分)求点P(-1,2)关于直线l:y=2x+1的对称点P的坐标。
20.(10分)分别求出经过直线l1:4x+3y-5=0和l2:3x+y+6=0的交点M,且满足下列条件的直线方程:
(1)经过点N(-3,2):(2)与原点的距离等于1。
21.(10分)某工厂计划生产某种产品500件,并把这500件产品平均分为若干批生产,已知每生产一批该产品既需要固定成本16万元,还需要活动成本S万元,S与每批产品的件数x的立方成正比,当生产一批产品为5件时,其活动成本为1万元。
(1)求每批产品的活动成本S与生产件数x的函数关系;
(2)问每批产品为多少件时,才能使生产这500件产品的总成本最低?
22.(8分)已知一元二次不等式ax2+bx+c>0中ac≠0。
(1)若x=2是该不等式的一个解,则一元二次不等式cx2+bx+a>0必有一个解为多少?并说明理由。
(2)若(m,n)是ax2+bx+c>0的解集,则cx2+bx+a>0的解集是什么?并说明理由。
(3)(本小问为附加题,4分)根据前两问,试给出关于不等式ax2+bx+c>0与cx2-bx+a>0解集之间关系的一个结论(只写出一个结论即可,不必给出所有情况)