参数方程极座标复习题84

84．直线的参数方程

一、典型例题

1．  过点M(2,1)作椭圆x²+4y²=16的弦AB，

（1）　　　 若M是AB的中点，求弦AB所在的直线方程；[x+2y-4=0]

（2）　　　 若AM=2BM，求弦AB所在的直线方程。[y=]

2．  过点P(,0)作倾倾角为a的直线与曲线x²+2y²=1交于M，N两点，求PM•PN的最小值及相应的a值。[6/5,p/6,5p/6]

3．  过双曲线的右焦点F作不垂直于x轴的直线交双曲线于M，N两点，弦MN的中垂线交x轴于R，求证：为定值。

4．  求直线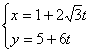（t为参数）与圆x²+y²=16的两个交点到点M(1,5)的距离的和与积。[5+1,10]

5．  过抛物线y²=4ax  (a>0)的焦点F的弦AB，设AB=l,O为坐标原点，⊿ABC的面积为S，当AB变化时，求证：为定值。[a³]

6．  已知抛物线y=x²-2x+2与直线y=kx (k>0)交于P₁，P₂两点，点Q在线段P₁P₂上，且满足，求点Q的轨迹方程。[2x+y-4=0(0<x<)]