83 曲线的方程的要领
一 典型例题
1． 化下列方程为普通方程：
（1）
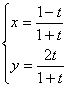（t为参数）
[x+y-1=0(x≠-1)]
（2）
（q为参数）
[5x2+4xy+17y2=81]
（3）
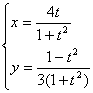（t为参数）
[x2/4+9y2=1(y≠-1/3)]
2．
分别在下列两种情况下，把参数方程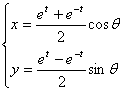
化为普通方程。
（1）q为参数，t为常数；（2）t为参数，q为常数。
3．
已知曲线C的普通方程为y=1-
，P(2,1)是曲线上的一点，Q(x,y)是曲线C上的点，弧长PQ的长为t，以t为参数，建立曲线C的参数方程。[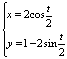
(t为参数0≤t≤2p)]
4． 证明：不论m为何值，双曲线x2-4y2-4mx+8(m+1)y-8m-84=0的两个焦点在两条平行直线上。
5．
在曲线
（q为参数）上求一点P，使它到直线x+2y+3=0的距离最小，并求出最小距离。[P(-
-1, -/2),2
/5]
6．
已知A，B分别是椭圆x2+4y2=4与圆x2+(y-2)2=
上的动点，求AB的最大值。[
]