高二上学期期中考试数学试卷
（统编新教材）
考试范围：第九章 立体几何、第十章 第一节 分类计数原理与分步计数原理
时量：120分钟 权值：150分 考试时间：
一、选择题(把正确的答案填入答卷的表中，每小题5分，共计60分)
1．经过空间任意三点作平面（ ）
A．只有一个 B．可作二个 C．可作无数多个 D．只有一个或有无数多个
2．两条异面直线在同一平面中的射影是（ ）
A．两条相交直线 B．两平行直线
C．两相交直线或平行直线 D．两相交直线或平行直线或一点和一直线
3．经过正棱锥S-ABC的高SO的中点且平行于底面的截面面积为1，则底面△ABC的面积为( ).
A.1 B
D.4
4．若
＝（2，1，1），
=(﹣１，x，1)且⊥ ，则x的值为( )
A．1 B．-1 C．2 D．0
5．若a =(2,﹣3,
)，b=(1，0，0)，则
=(
)
A．
B．
C．
D．
6．设三点A（1，1，0），B（1，0，1），C（0，1，1），则△ABC的形状为( )
A．Rt△ B．等边△ C．等腰△ D．等腰Rt△
7．两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm，把它们重叠在一起组成一
个新长方体，在这些新长方体中，最长的对角线的长度是( )
A．
B．
C．
D．
8．已知A、B、C不共线，O为平面ABC外的一点，满足（ ）的点M、A、B、C共面．
A．
B．
C．
D．
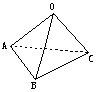
9．如图,正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于( )
(A)90° (B)60° (C)45° (D)30°
10．已知α，β是平面，m，n是直线.下列命题中不正确的是 （ ）
A．若m∥n，m⊥α，则n⊥α B．若m∥α，α∩β=n，则m∥n
C．若m⊥α，m⊥β，则α∥β D．若m⊥α，
，则α⊥β
11．一个长方体共一顶点的三个面的面积分别是
，这个长方体对角线的长是（ ）
A．
B．
C．6 D．
12．在正三棱柱
（ ）
A．60° （B）．90° （C）．105° （D）．75°
二、填空题（把正确的答案填入答卷的表中，每小题4分，共计16分）
13．已知：在空间四边形OABC中，OA⊥BC,OB⊥AC，
则OC与AB的夹角为_______.
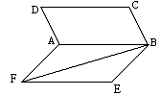
14．如右图所示，用五种不同的颜色，给标有A、B、C、D、E的各部分涂色，每一部分只能涂一种颜色，且要求相邻部分所涂颜色不同，则不同的涂色方法共有_________种.
15．已知某球体的体积与其表面积的数值相等，则此球体的半径为
.
16．如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面
角, 则异面直线AD与BF所成角的余弦值是
郴州市三中高二期中考试数学试卷答卷
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
第一、二大题答题表
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | ||||||||||||
| 题号 | 13 | 14 | 15 | 16 | ||||||||
| 答案 | ||||||||||||
三、解答题(共计74分)
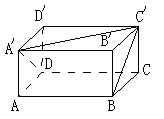
17．( 12分)如图，已知长方体的长宽都是4cm，高为2cm．
（1）求BC与
，
与
，
与所成角的余弦值；
（2）求与BC，与CD，与
所成角的大小．
18．( 12分)若平面α内的直角△ABC的斜边AB=20,平面α外一点O到A、B、C三点距离都是25,
求：点O到平面的距离．
19．（12分）如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC．DE垂直平分SC,且分别交AC、SC于
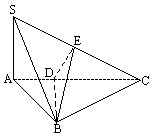D、E.又SA＝AB,SB＝BC.求: 二面角E-BD-C的度数。
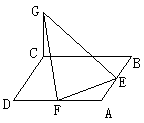20．（12分）已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC＝2.求：（1）点B到平面EFG的距离.（2）二面角C-EF-G的度数．
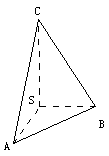
21．(13分)如图四面体S－ABC中，SA,SB,SC两两垂直, ∠SBA=45°, ∠SBC=60°，M为AB中点， (1) 求:AC与面SAB所成的角，(2) 求:SC与平面ABC所成角的正弦值．
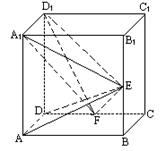22．(13分) 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(Ⅰ)证明AD⊥D1F; (Ⅱ)求AE与D1F所成的角;
(Ⅲ)证明面AED⊥面A1FD1;
郴州市三中高二2004年上学期期中考试数学试卷答案
一、选择题（每小题5分，共计60分)；二填空题（每小题4分，共计16分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | D | A | C | B | C | C | C | B | D | B |
| 题号 | 13 | 14 | 15 | 16 | ||||||||
| 答案 | 90° | 720 | 3 |
| ||||||||
三、解答题(共计74分)
17．( 12分)
解析：（1）
；
；
（2）90°；90°；0°
18．（12分） 解：由斜线相等，射影相等知，O在底面的射影为△ABC的外心Q，
又△ABC为Rt△外心在斜边中点，故OQ=
==
19．（12分）
解法一:由于SB＝BC,且E是SC的中点,因此BE是等腰三角形SBC的底边SC的中线,所以SC⊥BE.
又已知 SC⊥DE,BE∩DE＝E,
∴SC⊥面BDE, ∴SC⊥BD.
又 ∵SA⊥底面ABC,BD在底面ABC上, ∴SA⊥BD.
而SC∩SA＝S,∴BD⊥面SAC.
∵DE＝面SAC∩面BDE,DC＝面SAC∩面BDC, ∴BD⊥DE,BD⊥DC.
∴∠EDC是所求的二面角的平面角.
∵SA⊥底面ABC,∴SA⊥AB,SA⊥AC.
设SA＝a, 
又因为AB⊥BC,
∴∠ACS＝30°.
又已知DE⊥SC,所以∠EDC＝60°,即所求的二面角等于60°.
解法二:由于SB＝BC,且E是SC的中点,因此BE是等腰三角形SBC的底边SC的中线,所以SC⊥BE.
又已知SC⊥DE,BE∩DE＝E∴SC⊥面BDE, ∴SC⊥BD.
由于SA⊥底面ABC,且A是垂足,所以AC是SC在平面ABC上的射影.由三垂线定理的逆定理得BD⊥AC;又因E∈SC,AC是SC在平面ABC上的射影,所以E在平面ABC上的射影在AC上,由于D∈AC,所以DE在平面 ABC上的射影也在AC上,根据三垂线定理又得BD⊥DE.
∵DE
面BDE,DC面BDC, ∴∠EDC是所求的二面角的平面角.以下同解法一.
解法三:利用用向量求解：略
20．（12分） 解法一:
如图,连结EG、FG、EF、BD、AC.EF、BD分别交AC于H、O. 因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
BD不在平面EFG上.否则,平面EFG和平面ABCD重合,从而点G在平面的ABCD上,与题设矛盾.
由直线和平面平行的判定定理知BD∥平面EFG,
所以BD和平面EFG的距离就是点B到平面EFG的距离.
∵BD⊥AC ∴EF⊥HC. ∵GC⊥平面ABCD, ∴EF⊥GC,
∴EF⊥平面HCG. ∴平面EFG⊥平面HCG,HG是这两个垂直平面的交线.
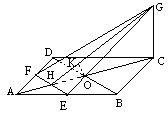作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,所以线段OK的长就是点B到平面EFG的距离.
解法二:利用用向量求解：略
21．(13分)解：①60°；
②解法一:连SM，CM， ∵∠SBA=45° ∴SM⊥AB, 又CS⊥AB, ∴AB⊥面CSM．
过S作CM的垂线SN，垂足为N，则SN⊥CM，SN⊥AB，∴SN⊥面ABC．
∠SCN为所求的线面角，设SB=1 则不难计算 CS=，SM=，CM=
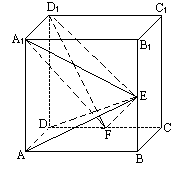sin∠SCM=
=
.
解法二:利用用向量求解：略
22．(13分) 解法一:
(Ⅰ)∵AC1是正方体,∴AD⊥面DC1. 又D1F面DC1, ∴AD⊥D1F.
(Ⅱ)取AB中点G,连结A1G,FG.因为F是CD的中点,所以GF、AD平行且相等,又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,A1G∥D1F.
设A1G与AE相交于点H,则∠AHA1是AE与D1F所成的角,因为E是BB1的中点,所以Rt△A1AG≌Rt△ABE,∠GA1A=∠GAH，从而
∠AHA1=90°,即直线AE与D1F所成角为直角.
(Ⅲ)由(Ⅰ)知AD⊥D1F,由(Ⅱ)知AE⊥D1F,又AD∩AE=A,所以D1F⊥面AED.又因为D1F面A1FD1,所以面AED⊥面A1FD1.
(Ⅳ)连结GE,GD1. ∵FG∥A1D1,∴FG∥面A1ED1, ∵AA1=2,
面积S△A1GE=S□ABB1A1-2S△A1AG--S△GBE=
又
解法二:利用用向量求解
解析：设正方体的棱长为2，以D为原点，DA为x轴，DC为y轴，DD1为z轴建立空间直角坐标系，则D（0，0，0），A（2，0，0），F（0，1，0），E（2，2，1），A1（2，0，2），D1（0，0，2），
(I) ∵ 
,
，得
，∴ AD⊥D1F;
(II)又
，得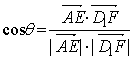
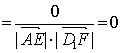
∴ AE与D1F所成的角为90°
(III) 由题意：
，
设平面AED的法向量为
，设平面A1FD1的法向量为
，
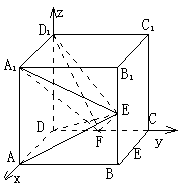由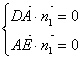
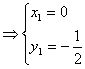
由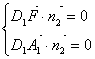
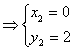
得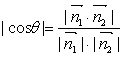
∴ 面AED⊥面A1FD1.
（Ⅳ）∵AA1=2，
，平面A1FD1的法向量为
， ∴E到平面A1FD1的距离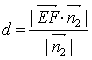
，
