2003年高二月考数学试卷
2003、10
一、选择题（每小题3分，满分36分）：
1．下列命题中，不成立的是（ ）
A) a>b,c<d
a-c>b-d B)
a>bc-a>c-b
C) a>b,ab>0
D)
a>b>0,c>d>0
2．若0<a<1,0<b<1 ,则a+b,2
,a2+b2,2ab中最大的一个数是（ ）
A) a + b B) 2
C) a2+b2 D) 2ab
3．下列不等式中，与不等式“x<3”同解的是（ ）
A) x+
<3+ B) x+
<3+
C) x(x+4)2<3(x+4)2 D) x(x-4)2<3(x-4)2
4．如果方程
的两个实根一个小于－1，一个大于1，那么实数m的取值范围为（ ）
A)
B)（－2，0） C)（－2，1） D)（0，1）
5．若函数f(x)=
的定义域为R，则实数k的取值范围是（ ）
A)0<k
1 B)k<0或k>1 C)0k1 D)k
1
6．图中的平面区域（阴影部分包括边界）可用不等式组表示为（ ）
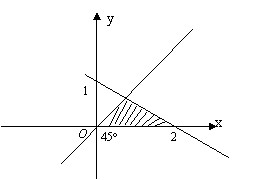A)
B)
C）
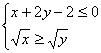D）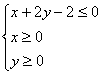
7．不等式
的解集是（ ）
A)
B)
C) 
D)
8．已知集合A＝
，B＝
且
，则a的取值范围是（ ）
A)
B)
C)
D) 
9．若A(－2,3),B(3,－2),C（0.5，m）三点在同一直线上，则m的值为（ ）
A)－2 B)2 C)－0.5 D)0.5
10．已知
，则直线
的倾斜角
的范围（ ）
A)
B)
C)
D)
11．已知l1：xsin+ycos+m=0，l2：x+ycot+n=0（为锐角，m，n∈R且m≠n） 则
与
的位置关系是（ ）
A)平行 B)垂直 C)重合 D)相交但不垂直
12．“m=2”是“直线 (m+2)x+my－3=0与mx－4y－1=0互相垂直”的（ ）
A)充分非必要条件 B)必要非充分条件
C)充要条件 D)即不充分也不必要条件
二、填空题：（每题3分，共15分）
13．已知直线
的方程是
则直线必经过点
14．已知点P（1，－2）及其关于原点的对称点均在不等式2x-by+1>0表示的平面区域内，则b的取值范围是
15．对于一切实数x,若
恒成立，则实数a的取值范围是
16．已知
17．一批货物随17列货车从A市以
千米/小时匀速直达B市，已知两地铁路线长为400千米，为了安全，两列货车的间距不得小于
千米，那么这批货物全部运到B市，最快需要小时。
2003年高二数学月考答卷
一、选择题（每小题3分，满分36分）：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题：（每题3分，共15分）
13． 14．
15． 16．
17．
三、解答题：
18．（本小题满分8分）
19．（本小题满分9分）光线从点A（2，3）射出，若镜面的位置在直线
上，反射线经过B（1，1），求入射线和反射线所在的直线的方程，并求光线从A
到B所走过的路线长。
20．（本小题满分10分）解关于x的不等式 
21．（本小题满分10分）某工厂在计划内要安排生产Ⅰ、Ⅱ两种产品，生产每件产品
需机时、工时、获利情况如下表，在不超过总机时100和总工时120的条件下，
应如何安排生产使获利最大，最大利润是多少？
| 机时 | 工时 | 获利（千元） | |
| Ⅰ | 2 | 4 | 6 |
| Ⅱ | 3 | 2 | 4 |
22．（本小题满分12分）设直线
过点P（2，1），按下列条件分别求直线的方程：
⑴直线与直线
的夹角为
⑵直线
与过点Q（1，3）的直线
平行，且与距离为2
⑶直线与两坐标轴的正向围成的三角形面积S最小。
附加题：（本小题满分10分，计入总分，但总分不超过100分）
设y=f(x)是定义在区间
上的函数，且满足条件：
Ⅰ)f(－1)=f(1)=0
Ⅱ)对任意的
都有
⑴证明对任意
，都有
⑵判断函数
是否满足题设条件。