高二复习概率题选

高二复习概率题选

1. 设只有颜色不同的3只球，每只球都以同样的可能性落入5个格子的每一个格子中，试求：

　　(1)某指定的3个格子中各有一只球的概率；　 （所求概率为P(A)＝=）

　　(2)3只球各在一个格子中的概率．　　　　  （所求概率P(B)= =。）

2．一袋中装有只黑球，只白球，它们大小相同，编号不同，现在把球随机地一只一只摸出来，求第次模出的球是黑球的概率(1≤≤+)．　　　　()

3．将大小相同但颜色不同的8只白乒乓球和2只黄乒乓球装入不透明的袋中，每次任意抽取一个辨别颜色，测试后不放回袋中，求下列事件的概率；

(1)抽三次，第三只是白乒乓球；　　　　　　　  (P（A）=或P（A）=)

  (2)直到第6只时才把两只黄乒乓球找出来．　　 (P（B）==)

4．从甲口袋内模出1个白球的概率是，从乙口袋内模出1个白球的概率是，从两个口袋内各模出1个球，那么是两个球　　　　　　　　　　　　　　　　　　　  ( B　 )

5．甲坛子中有3个白球，2个黑球；乙坛子中有1个白球，3个黑球；从这两个坛子中分别摸出1个球，假设每一个球被摸出的可能性都相等。问：

　　　 （1）它们都是白球的概率是多少？

　　　 （2）它们都是黑球的概率是多少？

　　　 （3）甲坛子中摸出白球，乙坛子中摸出黑球的概率是多少？

解：（1）显然，一次试验中可能出现的结果有n==20个,而这个事件包含的结果有m==3,根据等可能事件的概率计算公式得：P₁=。

（2）同（1）可得：P₂=。（3）同理：P₃=；

6．　同时投掷四枚均匀硬币一次，求：

(1)恰有两枚“正面向上”的概率：　　　　　　（P(A)＝．）

(2)至少有两枚“正面向上”的概率。　　　　  （P(B)＝）

7．　将一枚均匀硬币抛掷5次，

(1)求第一次、第四次出现正面，而另外三次都出现反面的概率；

　(2)求两次出现正面。三次出现反面的概率．

 解　(1)设第i次抛掷硬币出现正面事件记为A_i，表示第i次抛掷硬币出现反面的事件(i＝1，2，3，4，5)，则P(A_i)＝P()＝． 第一次、第四次出现正面，另外三次出现反面的事件为A₁A₄。

 则P(A₁A₄)＝P(A₁)P()P()P(A₄)P()＝××××=。

　 (2) P₅(2)＝　　　　　　　　　　

8．　袋中装有一等奖、二等奖、三等奖奖券各一张，每次任取一张，有放回地取三次，分别求下列事件的概率；

　　(1)取出的三张奖券等级是相问的：　　　  (P(A)＝＝)

　　(2)取出的三张奖券等级不全相问；　　　  (P(B)＝l一P(A)＝l一＝．)

　　(3)取出的三张奖券全是—等奖或全是二等奖．(十 =)

 9．　在100000张有奖明信片中。设有一等奖5个，二等奖l0个，三等奖100个，李明买了此种明信片10张，求：

　　(1)分别获一等奖、二等奖、三等奖的概率；　　(2)中奖的概率；　　(3)末中奖的概率．

　　解　（1）P_l＝＝； P₂＝＝； P₃=．

　　(2) P₄=P_l+ P₂+ P₃＝，　　(3)未中奖的概率P₅＝1一P₄＝1一＝．

 10．　同时抛掷两只均匀的骰子(各个面上分别标以数字l，2，3，4，5，6)，计算：

　　(1)　向上的数相同的概率；

　 （2）向上的数之积为偶数的概率；

　　(3)　向上的数之和不小于10的概率．

解　(1) P_l＝．　　　(2) P₂＝；得向上的数之积为偶数的概率P₃＝l一．

　　(3)　　十十＝

11．某商场为迎接国庆举办新产品问世促销 活动，方式是买—份糖果摸一次彩，模彩的器具是绿、白两色的乒乓球．这些乒乓球的大小和质料完全相同．商场拟按中奖率1％设大　奖，其余99％为小奖．为了制定摸彩的办法， 商场向职工广泛征集方案，对征集到的优秀　方案进行奖励．如果你是此商场职工，你将会提出怎样的方案?

注：商场提供的模彩器材是棱长约30cm 的立方体形木箱，密封良好，不透光、木箱上　方可容一只手伸入，另备足够多的白色乒乓球和少量绿色乒乓球。

方案一：　　在箱内放置100个乒乓球，其中1个为绿色乒乓球，其余99个为白色乒乓球，顾客一次模出1个乒乓球，如果为绿色乒乓球，即中大奖，否则中小奖，本方案中大奖的概率为：=。

　　方案二：　在箱内放置14个乒乓球，其中2个为绿色乒乓球，其余12个为白色乒乓球。顾客——次摸出2个乒乓球为绿色，即中大奖；如果模出的2个乒乓球为白色，或1个为白色、1个为绿色。则中小奖．本方案中大奖的概率=。

　　 方案三：在箱内放置15个乒乓球，其中2个为绵色乒乓球，其余13个为白色乒乓球．顾客摸球和中奖的办法与方案二相同．本方案中大奖的概率为=

　　方案四： 在箱内放置25个乒乓球，其中3个为绿色乒乓球，其余22个为白色乒乓球．顾客一次摸出2个乒乓球(或分两次模，每次摸一个乒乓球，不放回)，如果摸出的2个乒乓球为绿色，即中大奖；如果模出的2个乒乓球为白色或1个为白色、1个为绿色，则中小奖．本方案中大奖的概率为　　=。

12　设甲、乙两射手独立地射击同一目标，他们击中目标的概率分别为0.95，0.9．

求：(1)在一次射击中，目标被击中的概率；　　(2)目标恰好被甲击中的概率．

解　设甲击中目标事件为A，乙击中目标为事件B，根据题意，有P(A)＝0．95，P(B)＝0.9　

 (1)　　P(A·+·B+A·B)＝P(A·)十P(·B)十P(A·B) ＝P(A)·P()十P()·P(B)十P(A)·P(B)

　　　　＝0．95×(1—0．9)十(1—0．95)×O．9十0．95×0．90 ＝0．995。

(2) P(A·)＝P(A) ·P()＝0．95×(1一0。90)＝0．095．

13．　在人寿保险事业中，很重视某一年龄的投保人的死亡率，假如1个投保人能活到65岁的概率为0．6，试问；

　(1)3个投保人全部活到65岁的概率；　　　　  (P₃(3)＝=0.216；)

　(2)3个投保人有2个活到65岁的概率；　　　 (P₃(2)＝＝0．432；)

　(3)3个投保人有1个活到65岁的概率；　　　 (P₃(1)＝＝0．288；)

　(4)3个投保人都活不到65岁的概率．　　　　 (P₃(0)＝＝0．064。)

14　对某种药物的疗效进行研究，假定药物对某种疾病的治愈率为0．8，现在10个患此病的病人同时服用此药，求其中至少有6个病人治愈的概率．

　解：设病人服用该药后治愈记为事件A，没有治愈记为事件，则根据题意，有P(A)＝0．8，P()＝1一P(A)＝0。2．　至少有6个治愈可分为10人中6人治愈、7人治愈，8人治愈，9人治愈，10人治愈．

所以，所求概率为P＝P₁₀(6)+P₁₀ (7)十P₁₀ (8)十P₁₀ (9)十P₁₀ (10) ＝++++=0.97　　　　 

 15　某种大炮击中目标的概率是0.3，只要以多少门这样的大炮同时射击1次，就可以使击中目标的概率超过95％?

　 解　因为大炮击中目标的概率为0．3，所以大炮不击中目标的概率为0．7，n门大炮都击不中目标的概率是0.7ⁿ．因此，其中至少1门大炮击中目标的概率是1一0.7ⁿ，根据题意，有1一0.7ⁿ＞0．95，

即0.7ⁿ＜0．05， 两边取对数后，解不等式得 n＞ ．

即要以9门大炮同时射击1次，就可使击中目标的概率超过95％。

16．金工车间有10台同类型的机床，每台配备的电动机的功率为10千瓦。已知每台机床工作时，平均每小时实际开动12分钟，且开动与否是相互独立的。如因特殊情况，供电部门只提供50千瓦的电力给这10台机床，问这10台机床能够正常工作的概率为多大？

解：50千瓦可供给5台机床开动，因而10台机床中同时开动的台数不超过5台时都可以正常工作。又每台机床只有“开动”与“不开动”两种情况，且“开动”的概率为12/60=1/5，“不开动”的概率为4/5。

设10台机床中正在开动着的机床的台数为k，则

P(k)=,0≤k≤10

于是同时开动着的机床的台数不超过5台的概率为

P（k≤5）=　　　　　　　　  ≈0.994。

由此可知这10台机床的工作基本上不受电力供应紧张的影响，因为在电力供应为50千瓦的条件下，机床不能正常工作（同时开动6台或6台以上）的概率0.006，是一个小概率事件。

17． 甲、乙两名运动员进行乒乓球单打比赛。根据以往的比赛情况，每一局甲胜的概率为0.6，乙胜的概率为0.4。如果比赛时采用三局二胜制或五局三胜制，问哪一种赛制下甲胜的可能性较大？

解：（1）三局二胜制甲胜的概率=0.648。

（2）五赛三胜制甲胜的概率为=0.682。甲在“五局三胜”中获胜的可能性较大。

在第1，3，5，8路公共汽车都要停靠的一个站（假定这个站只能停靠一辆汽车），有18。一位乘客等候第1路或第3路汽车，假定当时各路汽车首先到站的可能性相等，求首先到站正好是这位乘客所要乘的汽车的概率。

解：由题意知共有4路车可在此站停靠，而且每路车首先到站的可能性相等，故基本事件共有4个，且每一个的发生都是等可能的，即基本事件总数=4。

设表示首先到站正好是1路或3路汽车这一事件，则所包含的基金事件数=2。故所求概率=

19．一批产品共100件，其中一等品有40件，二等品有60件，今从这批产品中任

意抽取3件，在下列抽取方式中，求抽出的三件中有两件是一等品，一件是二等品的概率。

有返回抽样：每次取一件，检查后放回，然后再抽取下一件。()

不返回抽样：每次抽取一件，检查后不放回，在剩下的产品中再抽取下一件。()

20．某参观团共有8人，将进入10个房间，如果每个房间进入人数不限，每人进入每个房间都是等可能的，求下列事件上的概率：

（1）=“某指定8房中各有1人”；　　　　 ()

（2）=“恰有8间房，其中各有1人”　　　 ()

（3）=“某指定房间中恰有3人”　　　　  ()

变1：如将第上题中的“房间”换成“车站”可改为如下形式：有8个乘客乘公共汽车，途经10个车站，假定每个乘客都可能在每个车站下车，试求下列事件的概率：

（1）=“在指定8个车站，每站下车1人”；

（2）=“恰有8个车站，每站下车 1人”

（3）=“某指定的车站恰有3人”

变2：将上例中的“10”换成正整数“”，将“8”换成正整数“”（ ≤）则具有以下形式：

　 将个不同的球随机地放入个盒子中去（≤）。假设每个盒子能容纳的球数不限，求下列事件的概率。

(1) 指定个盒子各一个球；（2）恰有个盒子各一个球。

解：把个盒子看作“房间”，球视为“人”，问题变为将“人”分配进“房间”，本题形似“摸球”而实际上属“分房问题”。

变3：将例中的“房间”换成“天”，“10”换成“365”，“8”换成“”则有如下的生日问题：

设有个人，≤365，并设每人的生日在一年的365天中的每一天是均等的，问此个人有不同生日的概率是多少？

解：所求概率的事件相当于例9中的事件，这里我们不妨仍设为，类似地例中的求法，

=

当较小时，

如取=2，得两人不同生日的概率为

 21．一架电梯开始时有6位乘客并停于十层楼的每一层，求下列事件的概率：

（1）“某指定的一层有两位乘客离开”　　　　　  （）

（2）“没有两位及两位以后的乘客在同一层离开”　 （）

（3）“恰有两位乘客的同一层离开”　　　　　　  (）

（4）“至少有两位乘客在同一层离开”　　　　　  （1－0.1512＝0.8488）

22．某产品中有15只正品，5只次品，每次取1只测试，取后不放回，直到5只次品全部测出为止，求经过10次测试，5只次品全部发现的概率。　　()

23．求所有三位数中，含有两个相同数字的三位数的概率。

分析： ==900，=243，这一步可分类计算：

0在内，则三位数形如：有27个；

0 不在内，则三位数形如：、是从1到9中任取2个，所以共有=216个，所以=27+216=243。　　  P(A)=

24．从5双不同号码的鞋子中任取4只，求这4只鞋子中至少有2只可配成一双的概率。

解：记事件=“4只鞋中至少有两只配成一双”， =“4只中恰好有2只配成一双”，=“4只中恰好配成两双”， 与互斥，=,事件包含的基本事件数

先从5双鞋中任选取一双，有种选法，把选中的一双2只都取出来有种选法，再在剩下的4双中任取2双有种选法，每双任取一只有种，所以有=

=

事件包含的基本事件数

先从5双中任取2双，有种选法，把选中的2双4只都取出来有种选法，所以=

=

∴＝＋＝＋＝

25．高二（8）班有6名同学是1988年9月份生的，求至少有2人是同一天生的概率。

解：记事件=“6人中至少有两人同一天出生”， =“6人中没有2人的生日相同”。九月份共30天，每个人可以是30天中任一天出生，全部可能的情况为=，没有二人生日相同，就是30天中取6个的排列数，得≈0.4136。

26．甲、乙两个篮球运动员，投篮的命中率分别为0.6和0.8。如果每人投篮两次。

（1）求甲投进2球，且乙投进1球的概率；

（2）若投进1个球得2分，未投进得0分，求甲、乙两人得分相等的概率。

0.1512  0.3924。

27．某厂生产的A产品按每盒10件进行包装，每盒产品均需检验合格后方可出厂．质检办法规定：从每盒10件A产品中任抽4件进行检验，若次品数不超过1件，就认为该盒产品合格；否则，就认为该盒产品不合格．已知某盒A产品中有2件次品．

（1）求该盒产品被检验合格的概率；

（2）若对该盒产品分别进行两次检验，求两次检验得出的结果不一致的概率．

解: (1) 被检验认为是合格的概率为…

(2)两次检验是相互独立的，可视为独立重复试验，

故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为

．

 28、用分层抽样法从10名男生5名女生中抽取3人参加智力游戏．试求某一男生甲以及某—女生乙分别被抽到的概率。　　　

 解∵抽样比为 ∴抽取男生×10＝2人　抽取女生× 5＝l人

　∴某男生甲被抽到的概率为P₁＝＝

　某女生乙被抽到的概率为P₂＝

29、某班50名学生，现在采用随机抽样方法逐一从中抽取5名同学参加夏令营，学生甲最后一个去抽，则他被拍中的概率为　　　　　　　　　　　　　　　　 

　(A)0．1　　　　　  (B)0．02　　　　  (C)0或1　　　　　  (D)以上都不对

　[分析]　因为用简单随机抽样从个体数为50的总体中抽取一个容量为5的样本，那么 每个个体被抽到的概率都等于＝，不论学生甲抽取的位置，他抽到参加夏令营的资格均为 ＝0．1．故选A．

30、在120个零件中．一级品24个，二级品36个，三级品60个，从中抽取容量为20的样本。

（1）　　　　 分别用简单随机抽样和分层抽样计算每个个体被抽到的概率。

（2）　　　　 用上述哪一种抽样使一级品中某甲与二级品中某乙都被抽到的概率较大。

 [解]　(1)用简单随机抽样，每个个体被抽到的概率为＝

　　 用分层抽样：一、二、三级品被抽取数分别为×24＝4，×36＝6，×60＝10。

故每层中每个个体被抽到的概率分别为，， 即都是。

 (2)用分层抽样时，因为在一级品抽样与在二级品中抽样是独立的，故一级品甲与二级　品乙都被抽到的概率为P＝·＝。

 用简单随机抽样时一级品甲与二级品乙都被抽到的概率为

　　P′＝＝×＜×=。

 故用分层抽样时，一级品甲与二级品乙都被抽到的概率较大．

31.某人忘记了电话号码的最后一个数字，因而他随意地拨号，假设拨过了的号码不再重复，试求下列事件的概率：

　 （1）第3次拨号才接通电话；

　 （2）拨号不超过3次而接通电话.

解：设A₁={第i次拨号接通电话}，i=1，2，3.

（1）第3次才接通电话可表示为于是所求概率为

（2）拨号不超过3次而接通电话可表示为：A₁+于是所求概率为

  P（A₁+）=P(A₁)+P()+P()=

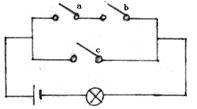
32.在如图所示的电路中，开关b，a，c开或关的概率都为，且相互独立，求灯亮的概率.

解法1：设事件A、B、C分别表示开关a,b,c关闭，则a,b同时关合或c关合时灯亮，即A·B·，A·B·C或·B·C，A··C，··C之一发生，又因为它们是互斥的，所以，所求概率为

　　P=P（A·B·）+P（·B·C）+P（A··C）+P（··C）+P（A·B·C）

　　 =P（A）·P（B）·P（）+P（）·P（B）·P（C）+P（A）·P（）·P（C）

　　　+P（）·P（）·P（C）+P（A）·P（B）·P（C）=

　　解法2：设A，B，C所表示的事件与解法1相同，若灯不亮，则两条线路都不通，即C一定开，a，b中至少有一个开.而a,b中至少有一个开的概率是

　　　　1－P（·）=1－P（）·P（）=，

　　所以两条线路皆不通的概率为

　　　　P（）·[1－P（·）]=

　　于是，灯亮的概率为.答：略.