高二数学综合练习（四）

高二数学综合练习（四）

班级＿＿＿＿姓名＿＿＿＿＿＿

一、选择题：

1．在4次独立重复试验中，随机事件A恰好发生1次的概率不大于其恰好发生两次的概率，则事件A在一次试验中发生的概率P的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　 　 (　　)

(A)[0，4，1]　　　　　 (B)(0，0．4)　　　　　 (C)(0，0．6)　　　  (D)[0．6，1]

2．由数字0，1，2，3，4，5可以组成无重复数字且奇偶数字相间的六位数的个数有　　　　　  （　 ）

A、72　　　　  B、60　　　　 C、48　　　　  D、52

　　　　　　　　　　　　　　　　　  　 （C）

3．3名男生与3名女生站在一排，如果要求男女生相间站，那么站法有　　　　　　　  　　　　（　 ）

　（A）36种　　　　  （B）72种　　　　　（C）108种　　 　　　（D）144种

4．在的展开式中，系数为有理数的项共有　　　　　　　　　　　　　　　　　  （　 ）

　（A）16项　　　　 （B）17项　　　　　 （C）18项　　　　　  （D）19项

5．M，N，P表示三个不同的平面，则下列命题中，正确的是　　　 　　　　　　　　　　　　  （　 ）

A．若M⊥P，N⊥P，则M∥N　　　　　　　　　　 B．若M⊥N，N∩P=φ，则M∩P≠φ

C．若M、N、P两两相交，则有三条交线　　　　 D．若N∩P=a，P∩M=b，M⊥N，则a⊥b

6．ABCD—A₁B₁C₁D₁是正方体，M、N分别是AA₁、BB₁的中点，设C₁M与DN所成的角为θ，则

sinθ的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

（A）．　　　　　 （B）．　　　　　　  （C）． 　　　　　 （D）．

7．某工厂生产的100件产品中，有95件正品，5件次品，从中任意取一件是次品的概率为　　　　（　 ）

 (A)  0．95　　　　　 (B)　95　　　　　 (C)　0．5　　　　  (D)0．05

8．函数＝x³—3x²—9x ＋3在区间[—2，2]上的最小值是　　　　　　　　　　　　  　(　　)

(A)l　　　　　　  (B)8　　　　　　 (C)一19　　　　　　　  (D)一24

9．对于可导函数，＝0是x₀为函数的极值点的　　　　　　 　　　　　　　　　 ( 　 )

　(A)充分非必要条件　 (B)必要非充分条件　　(C)充要条件　　(D)既不充分也不必要条件

10．正四面体的内切球球心到一个面的距离等于这个四面体高的　　　　　　　　　　　　　　　　 （　）

（A）　　　　　  （B）　　　　　　 （C）　　　　　　　　 （D）

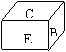
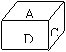11．一正方体的六个面上分别标有字母A、B、C、D、E、F，如图是此正方体的两种不同放置，则与D面相对的面上的字母是：　　　　　　　　　　　　　

（A）B　　　　　　　（B）E

（C）F　　　　　　　（D）以上三种情况均有可能

12．函数＝x³十ax²十bx十c，其中a，b，c为实数，当a²—3b＜0时，是　　　　　 (　　)

　　(A)增函数　　　　　  (B)减函数　　　　　　 (C)常数　　　　　　  (D)以上都不对

二、填空题：把答案填在题中横线上

13．已知函数y＝4(2x—1)², 当x＝＿＿＿＿＿时y′＝0。

14．设含有8个元素的集合的全部子集数为S，其中由3个元素组成的子集数为T，的值为___________。

15．已知母线长为10，底面半径为5的圆锥内有一球，球与圆锥的底面及圆锥的所有母线都相切，则球的体积是

16．的展开式中系数最大的项是第项。

三、解答题：解答应写出文字说明，证明过程或演算步骤

17．设函数y＝ax³十bx²十cx十d的图象与y轴交点为P且曲线在P点处切线方程为12x—y—4＝0．若函数在x＝2处取得极值0，试确定函数的解析式．

18．在120个零件中．一级品24个，二级品36个，三级品60个，从中抽取容量为20的样本。分别用简单随机抽样和分层抽样计算每个个体被抽到的概率。

用上述哪一种抽样使一级品中某甲与二级品中某乙都被抽到的概率较大。

　[

19．正三棱柱ABC—A₁B₁C₁中，AA₁=2AB，D、E分别是侧棱BB₁、CC₁上的点，且EC=BC=2BD，过A、D、E作一截面，求：

　 （Ⅰ）截面与底面所成的角；　 （Ⅱ）截面将三棱柱分成两部分的体积之比.

20．用0，1，2，3，4，5组成没有重复数字的自然数，

（1）　 有多少个比201 345大？

（2）有多少个是25的倍数的四位数？

21．已知的展开式的各项系数之和等于展开式中的常数项，求 展开式中含的项的二项式系数。

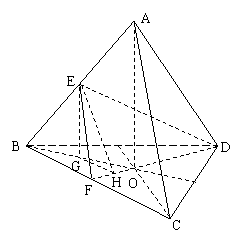
22．已知正三棱锥A-BCD的边长为a，E、F分别为AB、BC的中点，且AC⊥DE.

（Ⅰ）求此正三棱锥的体积；

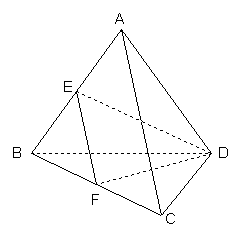（Ⅱ）求二面角E-FD-B的正弦值.

.

高二数学综合练习（四）答案

一、选择题： ABDBB　　DDCBC　　 AA

二、填空题： 13．1/2　　 14． 　　 15． 　　 16．　7

三、解答题：

17． y=2x³－9x²＋12x－4

18．

　[解]　(1)用简单随机抽样，每个个体被抽到的概率为＝

　　 用分层抽样：一、二、三级品被抽取数分别为×24＝4，×36＝6，×60＝10。

故每层中每个个体被抽到的概率分别为，， 即都是。

 (2)用分层抽样时，因为在一级品抽样与在二级品中抽样是独立的，故一级品甲与二级　品乙都被抽到的概率为P＝·＝。

 用简单随机抽样时一级品甲与二级品乙都被抽到的概率为

　　P′＝＝×＜×=。

 故用分层抽样时，一级品甲与二级品乙都被抽到的概率较大．

19．

解（Ⅰ）延长ED交CB延长线于F，

为截

面与底面所成二面角的平面角.　在Rt△AEC中，EC=AC，故得∠EAC=45°.

（Ⅱ）设AB=a，则，

．

.

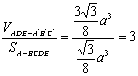
20．用0，1，2，3，4，5组成没有重复数字的自然数，

(1)　 119　　　(2)　21

21．

解：先求出的常数项是2⁷，从而可得中n=7，对于由二项展开式的通项公式知，含的项是第4项，其二项式系数是35。

22．

解：（Ⅰ）作AO⊥平面BCD于O,由正三棱锥的性质

可知O为底面中心，连CO,则CO⊥BD,由三垂线定理

知AC⊥BD，又AC⊥ED,∴AC⊥平面ABD,∴AC⊥AD,

AB⊥AC,AB⊥AD.在Rt△ACD中，由AC²+AD²=2AC²=a²

可得：AC=AD=AB=.

∴V=V_B-ACD=.

（Ⅱ）过E作EG⊥平面BCD于G，过G作GH⊥FD于H，连EH，由三垂线定理知EH⊥FD,即∠EHG为二面角E-FD-B的平面角.

∵EG＝AO 而AO＝,∴EG=.

又∵ED＝∵EF∥AC，∴EF⊥DE.∴在Rt△FED

中，EH＝∴在Rt△EGH中，sin∠EHG＝