高二文数学1、2、8班必修1复习卷1

高中数学必修1复习卷(A)

考号　　 班级　　　 姓名　　　　

一、选择题(每小题5分，共60分)

1．已知a＝，集合A＝{xx≤2}，则下列表示正确的是( 　)．

A．a∈A　　 B．a∈A　　 C．｛a｝∈A　　D．a⊆A

2．集合S＝｛a，b｝，含有元素a的S的子集共有（　 ）．

　　A．1个　　　　B．2个　　　　 C．3个　　　　 D．4个

3．已知集合M＝｛xx＜3｝，N＝｛xlog₂x＞1｝，则M∩N＝（ 　）．　 

A．Æ　　 B．｛x0＜x＜3｝ C．｛x1＜x＜3｝　D．｛x2＜x＜3｝

4．函数y＝的定义域是( 　)．

　　A．[4，＋∞)　 B．(4，＋∞)　　 C．(－∞，4］ 　D．(－∞，4)　

5．国内快递1000g以内的包裹的邮资标准如下表：

运送距离x (km)	0＜x≤500	500＜x≤1000	1000＜x≤1500	1500＜x≤2000	…
邮资y (元）	5.00	6.00	7.00	8.00	…

如果某人在南京要快递800g的包裹到距南京1200km的某地，那么他应付的邮资是(　　 )．

A．5.00元　　 B．6.00元　C．7.00元　　　D．8.00元

6．幂函数y＝x^a(a是常数)的图象（　　）．　

A．一定经过点(0，0) B．一定经过点(1，－1) C．一定经过点(－1，D．一定经过点(1，1)

7．0.4⁴，1与4^0.4的大小关系是（　　　 ）．

A．0.4⁴＜4^0.4＜1　　　B．0.4⁴＜1＜4^0.4 C．1＜0.4⁴＜4^0.4　　 D．l＜4^0.4＜0.4⁴

8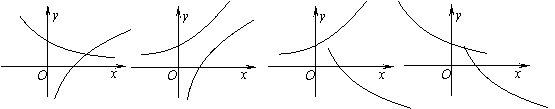．在同一坐标系中，函数y＝2与y＝logx的图象是(　　　)．

　　A．　　　　　　　  B．　　　　　　　  C．　　　　　　　　 D．

9．方程x³＝x＋1的根所在的区间是(　　)．

A．(0，1)　　　B．(1，2)　　 C．(2，3) 　　　D．(3，4)

10．下列函数中，在区间(0，＋∞)上是减函数的是（ 　）．

A．y＝－　　B．y＝x　 C．y＝x²　　　 D．y＝1－x

11．若函数f (x)＝＋a是奇函数，则实数a的值为 （　 ）．

A．　　　　B．－　　　　 C．2　　　　  D．－2

12．设集合A=｛0，1｝，B=｛2，3｝，定义集合运算：A⊙B＝｛z︳z= xy(x+y)，x∈A， y∈B｝，则集合A⊙B中的所有元素之和为（　 ）．

A．0　　　 B．6　　　　　 C．12　　　　　　　　 D．18

二、填空题（每小题5分，共30分）

13．集合S＝｛1，2，3｝，集合T＝｛2，3，4，5｝，则S∩T＝　 　　　　．

14．已知集合U＝｛x－3≤x≤3｝，M＝｛x－1＜x＜1｝，_UM＝　　　　　 ．

15．如果f (x)＝那么f (f (1))＝　　　　　　 ．

16．若函数f(x)＝ax³＋bx＋7，且f(5)＝3，则f(－5)＝__________．

17．已知2^x＋2^－x＝5，则4^x＋4^－x的值是　　　　　 ．

18．在下列从A到B的对应： (1)A＝R，B＝R，对应法则f：x→y＝x² ； (2) A＝R，B＝R，对应法则f：x→y＝； (3)A＝(0，+∞)，B＝{yy≠0}，对应法则f：x→y＝±；(4)A＝N^*，B＝{－1，1}，对应法则f：x→y＝(－1)^x　其中是函数的有　　　　　　　　 ．（只填写序号）

三、解答题（共70分）

19．（本题满分10分）计算：2log₃2－log₃＋log₃8－．

20．（本题满分10分）已知U＝R，A＝｛x－1≤x≤3｝，B＝｛xx－a＞0｝．

(1)若AÍB，求实数a的取值范围；

(2) 若A∩B≠Æ，求实数a的取值范围．

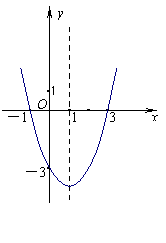21．（本题满分12分）已知二次函数的图象如图所示．

（1）写出该函数的零点；

（2）写出该函数的解析式．

22．（本题满分12分）已知函数f(x)＝lg(2＋x)，g(x)＝lg(2－x)，设h(x)＝f(x)＋g(x)．

(1)求函数h(x)的定义域；

(2)判断函数h(x)的奇偶性，并说明理由．

23．（本题满分12分）销售甲、乙两种商品所得利润分别是P(万元)和Q(万元)，它们与投入资金t(万元)的关系有经验公式P＝，Q＝t．今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资x(万元)．

求：(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式；

(2)总利润y的最大值．

24．（本题满分14分）已知函数f (x)＝．

(1)判断f (x)在区间(0，＋∞)的单调性，并用定义证明；

(2)写出函数f (x)＝的单调区间．

试卷答案必修1(A)

一、选择题(每小题5分，共60分)

1．A　2．B　 3． D　 4．C　 5．C　 6．D　 7．B　8．A　9．B　10．D　11．A　 12．D

二、填空题（每小题5分，共30分）

13．｛2，3｝14．[－3，－1]∪[1，3]　 15．5　 16．11　17．23　 18．(1)(4)

三、解答题（共70分）

19．解 原式＝log₃4－log₃＋log₃8－3＝log₃(4××8)－3＝log₃9－3＝2－3＝－1．

20．解（1）B＝｛xx－a＞0｝＝｛xx＞a｝．由AÍB，得a＜－1，即a的取值范围是｛a a＜－1｝；（2）由A∩B≠Æ，则a＜3，即a的取值范围是｛a a＜3｝．

21．（1）函数的零点是－1，3；

（2）函数的解析式是y＝x²－2x－3．

22．解(1)由 得－2＜x＜2．所以函数h(x)的定义域是{x－2＜x＜2}．

(2) ∵h(－x)＝lg(2－x)＋lg(2＋x)＝h(x)，∴h(x)是偶函数．

23．解(1)根据题意，得y＝＋(3－x)，x∈［0，3］．

(2) y＝－(－)²＋．

∵∈［0，3］，∴当＝时，即x＝时，y_最大值＝．

答：总利润的最大值是万元．

24．解(1) f (x)在区间(0，＋∞)为单调减函数．证明如下：

 设0＜x₁＜x₂，f (x₁)－f (x₂)＝－＝＝．

因为0＜x₁＜x₂，所以(x₁x₂)²＞0，x₂－x₁＞0，x₂＋x₁＞0，即＞0．

所以f (x₁)－f (x₂) ＞0，即所以f (x₁) ＞f (x₂)，f (x)在区间(0，＋∞)为单调减函数．

(2) f (x)＝的单调减区间(0，＋∞)；f (x)＝的单调增区间(—∞，0)．