高二文科数学下期第二次月考试题 数学(文科)
时间:120分钟 满分:160分
一. 填空题(本题共14小题,每题5分,共70分):
1.已知集合![]() ,集合
,集合![]() ,则
,则![]() = .
= .
2.函数![]() 的定义域是
.
的定义域是
.
3.![]() 是纯虚数,则实数
是纯虚数,则实数![]() 的值是___________.
的值是___________.
4.把正整数按下图所示的规律排序,则从2003到2005的箭头方向依次为

5.函数![]() 的图象和函数
的图象和函数![]() 的图象的交点个数是
.
的图象的交点个数是
.
6.已知![]() 是偶函数,定义域为
是偶函数,定义域为![]() ,则
,则![]() = .
= .
7.已知![]() ,则
,则![]() 等于
等于
8.某医疗机构通过抽样调查(样本容量![]() ),利用
),利用![]() 列联表和卡方统计量研究患肺病是否与吸烟有关.计算得
列联表和卡方统计量研究患肺病是否与吸烟有关.计算得![]() ,经查对临界值表知
,经查对临界值表知![]() ,则下列结论中正确的是
,则下列结论中正确的是
A.在100个吸烟的人中约有95个人患肺病
B.若某人吸烟,那么他有![]() 的可能性患肺病
的可能性患肺病
C.有![]() 的把握认为“患肺病与吸烟有关”
的把握认为“患肺病与吸烟有关”
D.有![]() 的把握认为“患肺病与吸烟有关”
的把握认为“患肺病与吸烟有关”
9.二次函数![]()
![]() ,则函数的值域是
。
,则函数的值域是
。
10.已知定义在实数集R上的偶函数![]() 在区间
在区间![]() 上是单调增函数,若
上是单调增函数,若![]() ,则
,则![]() 的取值范围是 ▲ .
的取值范围是 ▲ .
11.已知![]() ,且函数
,且函数![]() 的最小正周期是
的最小正周期是![]() . 类比上述结论,若
. 类比上述结论,若![]() ,
,![]() 为正的常数,且有
为正的常数,且有 ![]() ,则
,则![]() 的最小正周期是
.
的最小正周期是
.
 12.若命题“
12.若命题“![]() ,使得
,使得![]() ”是真命题,则实数
”是真命题,则实数![]() 的取值范围是 .
的取值范围是 .
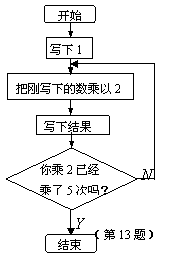
13.按右图所示的流程图操作,操作结果是
14.从![]() 中,可得到一般规律为 .(用数学表达式表示)
中,可得到一般规律为 .(用数学表达式表示)
二. 解答题(共6小题,共90分,解答时应写出文字说明,证明过程或演算步骤):
15.(本题14分)已知复数![]() 满足
满足![]() 且
且![]() 为实数,求
为实数,求![]() .
.
16.(本题14分)定义运算![]() ,集合
,集合![]() ,
,![]() ,求:
,求:![]() 与
与![]() .
.
17.(本题14分)设![]() 求证:
求证:![]() 。
。
18.(本题16分)一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(1)变量y对x进行相关性检验;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?
19.(本题16分)已知![]() .
.
(1)证明:函数![]() 在
在![]() 上为增函数;
上为增函数;
(2)用反证法证明:方程![]() 没有负数根.
没有负数根.
20.(本题16分)已知二次函数![]() 满足:对任意实数x,都有
满足:对任意实数x,都有![]() ,且当
,且当![]() (1,3)时,有
(1,3)时,有![]() 成立.
成立.
(1)证明:![]() ;
;
(2)若![]() 的表达式;
的表达式;
(3)在(2)的条件下,设![]()
![]() ,若
,若![]() 图上的点都位于直线
图上的点都位于直线![]() 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
参考答案:
一.填空题:
1.![]() 2.
2. ![]() ∪
∪![]() 3. 1 4. B 5. 3 6.
3. 1 4. B 5. 3 6. ![]() 7
7 ![]() 8. C 9.
8. C 9. ![]() 10.
10.
![]() 11.
11. ![]() 12.
12. ![]() 13. 1,2,4,8,16,32
13. 1,2,4,8,16,32
14. ![]()
二.解答题:
15. ![]()
16. ![]()
∴ ![]() 即
即![]() …………6分
…………6分
∵
![]() ,∴
,∴ ![]()
∴ ![]() ,则
,则![]()
即![]() ………10分
………10分
∴![]()
![]() ………14分
………14分
17. 证明:要证明![]() ,只要证明
,只要证明![]() ,
,
即证明![]() ,
,![]() ,
,![]()
即证明![]() ,只要证明
,只要证明![]() ,
,
![]() ∴
∴![]() ,
,![]() ∴
∴![]()
∴![]() 是成立的,由于上述步步可逆,∴
是成立的,由于上述步步可逆,∴![]() 成立.
成立.
……14分
18. 解:(1)r=0.995,所以y与x有线性性相关关系 ----------4分
(2)y=0.7286x-0.8571 ----------8分
(3)x小于等于14.9013 ----------12分
19. 证明:(1)![]() .…………4分
.…………4分
![]() ,
,![]() ,
,![]() ,………6分
,………6分
![]() ,
,![]() 函数
函数![]() 在
在![]() 上为增函数;……8分
上为增函数;……8分
(2)假设存在![]() ,满足
,满足![]() ,………10分
,………10分
则![]() ,
,![]() ,
,![]() ,………13分
,………13分
解得![]() ,与假设
,与假设![]() 矛盾.故方程
矛盾.故方程![]() 没有负数根.…16分
没有负数根.…16分
20. (1)由条件知 ![]() 恒成立
恒成立
又∵取x=2时,![]() 与恒成立
与恒成立
∴![]() …………4分
…………4分
(2)∵![]() ∴
∴![]()
∴![]() ……6分
……6分
又 ![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
∴![]() , …………10分
, …………10分
解出:![]() ,∴
,∴![]() …………12分
…………12分
(3)由分析条件知道,只要![]() 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 ![]() 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率![]() 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是:
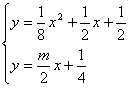 利用相切时△=0,解出
利用相切时△=0,解出 ![]()
∴![]() …………16分
…………16分