绝密★启用前 试题类型:A
高二文科数学第二学期期末调研测试题
数学试题(文科)2008.07
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。满分150分,考试时间120分钟。
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡
皮擦干净后,再选涂其他答案,不能答在试题卷上.
3.考试结束,监考人将本试卷和答题卡一并收回.
参考公式
![]() ,其中n=a+b+c+d为样本量
,其中n=a+b+c+d为样本量
相关系数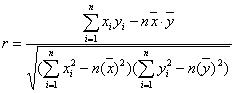
求线性回归方程系数公式 :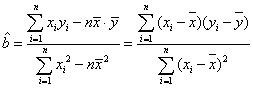 ,
,![]() .
.
可信程度表:
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
第Ⅰ卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1、复数![]() 的虚部是( )
的虚部是( )
A、![]() B、
B、![]() C、
C、![]() D、1
D、1
2、已知等差数列{an}的前n项和为![]() ,若
,若![]() , 则
, 则![]() 等于 ( )
等于 ( )
A、72 B 、
3、已知![]() 、
、![]() 均为单位向量,它们的夹角为60°,那么
均为单位向量,它们的夹角为60°,那么![]() =( ).
=( ).
A、![]() B、
B、![]() C、
C、![]() D、4
D、4
4、已知回归直线斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、设Sn是等差数列![]() 的前n项和,若
的前n项和,若![]() ( )
( )
A、1 B、-![]()
6、两个变量![]() 与
与![]() 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数![]() 如下 ,其中拟合效果最好的模型是( )
如下 ,其中拟合效果最好的模型是( )
A、模型1的相关指数![]() 为0.98 B、模型2的相关指数
为0.98 B、模型2的相关指数![]() 为0.80
为0.80
C、模型3的相关指数![]() 为0.50 D、模型4的相关指数
为0.50 D、模型4的相关指数![]() 为0.25
为0.25
7、使复数为实数的充分而不必要条件是( )
A、 ![]() B、
B、 ![]() C、
C、![]() 为实数
为实数 ![]() D、
D、![]() 为实数
为实数
8、设α、β是方程![]() 的两根,且α、α+β、β成等比数列,则k的值为 ( )
的两根,且α、α+β、β成等比数列,则k的值为 ( )
A、2
B、
9、P是△ABC所在平面上一点,若![]() ,则P是△ABC的( )
,则P是△ABC的( )
A、外心 B、内心 C、重心 D、垂心
第1页(共9页)
10、下面使用类比推理恰当的是 ( )
A、“若![]() ,则
,则![]() ”类推出“若
”类推出“若![]() ,则
,则![]() ”
”
B、“若![]() ”类推出“
”类推出“![]() ”
”
C、“若![]() ” 类推出“
” 类推出“![]() (c≠0)”
(c≠0)”
D、“![]() ” 类推出“
” 类推出“![]() ”
”
11、设平面向量![]() =(-2,1),
=(-2,1),![]() =(λ,-1),若
=(λ,-1),若![]() 与
与![]() 的夹角为钝角,则λ的取值范围是( )
的夹角为钝角,则λ的取值范围是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
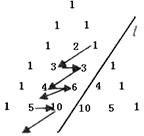
12、如图,在杨辉三角形中,斜线l的上方,从1开始
箭头所示的数组成一个锯齿形数列:1,3,3,4,
6,5,10,…,记其前n项和为Sn,
则S19等于( )
 A、129 B、172
A、129 B、172
C、228 D、283
第2页(共9页)
绝密★启用前 试题类型:A
高二期末调研测试题
数学试题(文科) 2008.07
|
注意事项:
1.第Ⅱ卷共7页,用钢笔或圆珠笔直接答在试题卷中.
2.答卷前将密封线内的项目填写清楚.
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 得分 | ||||||||
二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上.
| 非统计专业 | 统计专业 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
13、某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:为了检验主修统计专业是否与性别有关系,根据表中的数据,得到
![]() .因为K2≥3.841,所以断定主修统计专业与性别有关系,这种判断出错的可能性为
。
.因为K2≥3.841,所以断定主修统计专业与性别有关系,这种判断出错的可能性为
。
14、数列{an}中,![]() 的前n项的和为
。
的前n项的和为
。
15、已知向量![]() ,且A、B、C三点共线,则k= .
,且A、B、C三点共线,则k= .
![]()
![]() 第3页(共9页)
第3页(共9页)
16、用一条直线截正方形的一个角,得到边长为a,b,c的直角三角形(图1);用一个平面截正方体的一个角,得到以截面为底面且面积为S,三个侧面面积分别为S1,S2,S3的三棱锥(图2). 试类比图1的结论,写出图2的结论.
|
三、解答题:本大题共6小题,共74分. 解答应写出文字说明、证明过程或演算步骤.
17、(本小题满分12分)
已知复数![]() 满足:
满足: ![]() 求
求![]() 的值.
的值.
第4页(共9页)
18、(本小题满分12分)
设向量![]() ,向量
,向量![]() 垂直于向量
垂直于向量![]() ,向量
,向量![]() 平行于
平行于![]() ,
,
试求![]() 的坐标.
的坐标.
第5页(共9页)
19、(本小题满分12分)
已知各项均为正数的数列{![]() }的前n项和满足
}的前n项和满足![]() ,
,
且![]()
(Ⅰ)求a1;(Ⅱ)证明{![]() }是等差数列并求数列的通项公式。
}是等差数列并求数列的通项公式。
第6页(共9页)
![]()
20、(本小题满分12分)
已知:![]() 、
、![]() 、
、![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中![]() =(1,2)
=(1,2)
⑴若![]()
![]() ,且
,且![]() ,求
,求![]() 的坐标;
的坐标;
![]() ⑵若
⑵若![]() =
=![]() 且
且![]() 与
与![]() 垂直,求
垂直,求![]() 与
与![]() 的夹角θ.
的夹角θ.
第7页(共9页)
21、(本小题满分12分)
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
|
| 2 | 3 | 4 | 5 | 6 |
|
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程![]() ;
;
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
(![]() )
)
第8页(共9页)
22、(本小题满分14分)
数列{![]() }中,
}中,![]() =8,
=8,![]() =2,且满足
=2,且满足![]() (n∈N*).
(n∈N*).
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() =
=![]() +
+![]() +…+
+…+![]() ,求
,求![]() ;
;
(3)设![]() =
=![]() (n∈N*),
(n∈N*),![]() (n∈N*),是否存在最大的整数m,使得对任意n∈N*,均有
(n∈N*),是否存在最大的整数m,使得对任意n∈N*,均有![]() 成立?若存在,求出m的值;若不存在,请说明理由.
成立?若存在,求出m的值;若不存在,请说明理由.
第9页(共9页)
文科数学参考答案
1-5 B A C C A 6
13、 0.05 14、![]() 15、
15、![]() 16、
16、![]()
17、解:设![]() ,而
,而![]() 即
即![]()
则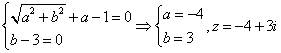
18、解:设![]() ,∴
,∴![]() ,∴
,∴![]() ①
①
又![]() 即:
即:![]() ②
②
联立①、②得![]() ∴
∴ ![]() .
.
![]()
19、解:由![]() ,解得a1=1或a1=2,
,解得a1=1或a1=2,
由假设a1=S1>1,因此a1=2。
(Ⅱ)由an+1=Sn+1-Sn=![]() ,
,
得an+1- an-3=0或an+1+an=0
因an>0,故an+1=-an不成立,舍去。
因此an+1- an-3=0。从而{an}是公差为3,首项为2的等差数列,
故{an}的通项为an=3n-1。
20、解:⑴设![]()
![]()
由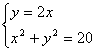 ∴
∴![]() 或
或 ![]()
∴![]()
⑵![]()
![]() ……(※)
……(※)
![]() 代入(※)中,
代入(※)中,
![]()
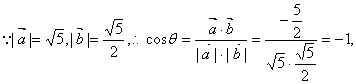
![]()
21、解:(Ⅰ)图……………………3分
(Ⅱ)依题列表如下:
|
| 1 | 2 | 3 | 4 | 5 |
|
| 2 | 3 | 4 | 5 | 6 |
|
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
|
| 4.4 | 11.4 | 22.0 | 32.5 | 42.0 |
|
| |||||
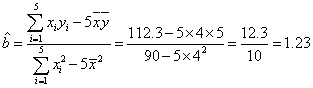 .
.
![]() .
.
![]() 回归直线方程为
回归直线方程为![]() .………………10分
.………………10分
(Ⅲ)当![]() 时,
时,![]() 万元.
万元.
即估计用10年时,维修费约为12.38万元.………………12分
22、解 (1)由![]() 知,数列{
知,数列{![]() }为等差数列,设其公差为d,则d=
}为等差数列,设其公差为d,则d=![]() ,
,
故![]() .
.
(2)由![]() ≥0,解得n≤5.故
≥0,解得n≤5.故
当n≤5时,![]() =
=![]() +
+![]() +…+
+…+![]() =
=![]() +
+![]() +…+
+…+![]() =
=![]() ;
;
当n>5时,![]() =
=![]() +
+![]() +…+
+…+![]() =
=![]() +
+![]() +…+
+…+![]() -…-
-…-![]() =
=![]() .
.
(3)由于![]() =
=![]() ,
,
所以![]() ,
,
从而![]() >0.
>0.
故数列![]() 是单调递增的数列,又因
是单调递增的数列,又因![]() 是数列中的最小项,要使
是数列中的最小项,要使![]() 恒成立,则只需
恒成立,则只需![]() 成立即可,由此解得m<8,由于m∈Z,故适合条件的m的最大值为7.
成立即可,由此解得m<8,由于m∈Z,故适合条件的m的最大值为7.