(圆锥曲线)
班级 学号 姓名
一 选择题(3×12=36`)
1.抛物线![]() 的准线方程是 ( )
的准线方程是 ( )
(A) ![]() (B)y=2 (C)
(B)y=2 (C)![]() (D)y=4
(D)y=4
2.双曲线![]() 的渐近线方程是( )
的渐近线方程是( )
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.已知双曲线![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 的离心率为 ( )
的离心率为 ( )
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4. 平面内两定点A、B及动点P,设命题甲是:“PA+PB是定值”,命题乙是:“点P的轨迹是以A.B为焦点的椭圆”,那么 ( )
A.甲是乙成立的充分不必要条件 B.甲是乙成立的必要不充分条件
C.甲是乙成立的充要条件 D.甲是乙成立的非充分非必要条件
5.双曲线![]() 的一个焦点是(0,-3),则m的值为( )
的一个焦点是(0,-3),则m的值为( )
(A) -1 (B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
6.顶点在原点,以x轴为对称轴的抛物线上一点的横坐标为6,此点到焦点的距离等于10,则抛物线焦点到准线的距离等于( )
(A) 4 (B)8 (C)16 (D)32
7..曲线![]() 与
与![]() (m>-16且
(m>-16且![]() ) ( )
) ( )
(A) 有相同的实轴 (B)有相同的焦距 (C)有相等的离心率 (D)有相同的准线
8 若椭圆![]() ,
,![]() F为靠近A点的焦点,若
F为靠近A点的焦点,若![]() ,则此椭圆的离心率为 ( )
,则此椭圆的离心率为 ( )
(A) ![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
9. ![]() 为双曲线
为双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() ,则
,则![]() 的面积是( )
的面积是( )
(A) 2 (B)4 (C)8 (D)16
10.如果双曲线![]() 上一点P到它的右焦点的距离为8,那么点P到它的左准线的距离为( )
上一点P到它的右焦点的距离为8,那么点P到它的左准线的距离为( )
(A)
![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.过点P(4,4)与双曲线![]() 只有一个公共点的直线有( )条
只有一个公共点的直线有( )条
(A) 1 (B) 2 (C)3 (D)4
12抛物线![]() 上到直线
上到直线![]() 的最短距离是( )
的最短距离是( )
(A) ![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(4`×4=16`)
13![]() 交抛物线
交抛物线![]() 于A,B两点,若AB中点的横坐标是2,则
于A,B两点,若AB中点的横坐标是2,则![]() ________.
________.
14. 已知抛物线型拱桥的顶点距离水面![]() 米后,水面的宽度是____.
米后,水面的宽度是____.
15.与圆![]() 外切且与圆
外切且与圆![]() 内切的动圆圆心轨迹为______________.
内切的动圆圆心轨迹为______________.
16圆心在抛物线![]() 上,并且与抛物线的准线及y轴都相切的圆的方程是__
_.
上,并且与抛物线的准线及y轴都相切的圆的方程是__
_.
三、解答题
17:求与双曲线![]() 有共同的渐近线,并且经过点
有共同的渐近线,并且经过点![]() 的双曲线方程.(
的双曲线方程.( ![]() )
)![]()
18.已知双曲线的左右焦点分别为![]() ,离心率为
,离心率为![]() 且过点(4,-
且过点(4,-![]() )。(
)。( ![]() )
)
(1)求双曲线的标准方程。(2)直线x=3与双曲线交于M、N两点,求证:![]()
19. 已知双曲线的中心在原点,对称轴为坐标轴,焦点在x轴上,两准线间的距离为![]() ,并且与直线
,并且与直线![]() 相交所得线段中点的横坐标为
相交所得线段中点的横坐标为![]() ,求这个双曲线方程.(
,求这个双曲线方程.(![]() )
)
20. 抛物线![]() 上有两个定点A、B分别在对称轴的上下两侧,F为抛物线的焦点,并且FA=2,FB=5,在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.(
上有两个定点A、B分别在对称轴的上下两侧,F为抛物线的焦点,并且FA=2,FB=5,在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.(![]() )
)
21.已知圆锥曲线![]() 的一个焦点为
的一个焦点为![]() (1,0),对应这个焦点的准线方程为
(1,0),对应这个焦点的准线方程为![]() ,又曲线过
,又曲线过![]() ,AB是过F的此圆锥曲线的弦;圆锥曲线
,AB是过F的此圆锥曲线的弦;圆锥曲线![]() 中心在原点,其离心率
中心在原点,其离心率![]() ,一条准线的方程是
,一条准线的方程是![]() 。(1)求圆锥曲线
。(1)求圆锥曲线![]() 和
和![]() 的方程。(2)当
的方程。(2)当![]() 不超过8,且此弦所在的直线与圆锥曲线
不超过8,且此弦所在的直线与圆锥曲线![]() 有公共点时,求直线AB的倾斜角
有公共点时,求直线AB的倾斜角![]() 的取值范围。(
的取值范围。(![]() )
)
蓬安中学高2009级数学单元测试(圆锥曲线)答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | C | B | A | B | B | A | B | D | C | A |
二、13.![]()
![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
17.解:由题意可设所求双曲线方程为:![]()
![]() 双曲线经过点
双曲线经过点![]()
![]()
![]()
![]() 所求双曲线方程为:
所求双曲线方程为:![]()
18.解:![]()
![]() ⑴设双曲线的标准方程为:
⑴设双曲线的标准方程为:![]() ,把点
,把点![]() 代入上方程得:
代入上方程得:![]() 所以所求双曲线的标准方程为
所以所求双曲线的标准方程为![]() 。
。
 ⑵由
⑵由![]() 得
得![]() ,由
,由![]() 得(如图)
得(如图)
![]() 。
。![]()
![]()
![]() 此题结论不成立。
此题结论不成立。
19.解: 由题意可设所求双曲线方程为:![]() 设直线
设直线![]() 与双曲线相交于
与双曲线相交于![]() ,
,![]() ,则
,则 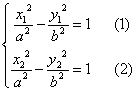 (1)-(2)得:
(1)-(2)得:![]() 即
即![]() 又由线段AB中点的横坐标为
又由线段AB中点的横坐标为![]() 可得,其纵坐标为
可得,其纵坐标为![]()
![]()
![]()
![]() 又
又![]()
![]()
![]()
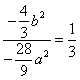
![]()
![]() ,
,![]() ,
,![]() 又
又![]() 双曲线两准线间的距离为
双曲线两准线间的距离为![]()
![]()
![]()
![]()
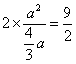
![]()
![]()
![]()
![]()
![]()
![]() 所求双曲线方程为:
所求双曲线方程为:![]()
20.解:由已知得![]() ,不妨设点A在x轴上方且坐标为
,不妨设点A在x轴上方且坐标为![]() ,由
,由![]() 得
得![]()
所以A(1,2),同理B(4,-4), 所以直线AB的方程为![]() .设在抛物线AOB这段曲线上
.设在抛物线AOB这段曲线上
![]() ,且
,且![]() .
.
则点P到直线AB的距离d=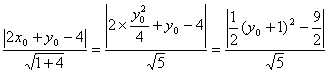
所以当![]() 时,d取最大值
时,d取最大值![]() ,又
,又![]() 所以△PAB的面积最大值为
所以△PAB的面积最大值为![]() 此时P点坐标为
此时P点坐标为![]() .
.
21.解:⑴过P作直线x=-1的垂线段PN.![]() 曲线
曲线![]() 是以
是以![]() 为焦点,x=-1为准线的抛物线,且
为焦点,x=-1为准线的抛物线,且![]() .
.![]() 曲线
曲线![]() ;
;
依题意知圆锥曲线![]() 为椭圆,
为椭圆,![]()
![]()
![]() .又其焦点在y轴上,
.又其焦点在y轴上,![]() 圆锥曲线
圆锥曲线![]() :
:![]()
(2)设直线AB:![]() ,
,![]() .由抛物线定义得:
.由抛物线定义得:![]() ,
,
又由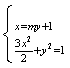 得
得![]() ,其
,其![]() 时,
时,![]() 。
。
依题意有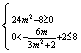 即
即![]() ,则
,则![]()
![]() 直线AB的倾斜角
直线AB的倾斜角![]() 。
。