高二级数学立体几何第三单元测试题(120分钟)
班级 姓名__________ 学号_______
一、选择题(本大题共10小题,每小题3分,共30分)
1.在一个45°的二面角的一个面内有一条直线与二面角的棱成45°角,则此直线与二面角的另一个面所成的角为( )
A.30° B.45° C.60° D.90°
2.已知二面角α—AB—β是直二面角,P为棱AB上一点,PE、PF分别在面α、β内,∠EPB=∠FPB =45°,那么∠EPF的大小是( )
A.60° B.45° C.120° D.不能确定
3.已知直线![]() ⊥平面α,直线m
⊥平面α,直线m![]() 平面β,有下列四个命题:①α∥β
平面β,有下列四个命题:①α∥β![]()
![]() ⊥m;②α⊥β
⊥m;②α⊥β![]()
![]() ∥m;③
∥m;③![]() ∥m
∥m![]() α⊥β;④
α⊥β;④![]() ⊥m
⊥m![]() α∥β,其中正确的两个命题是(
)
α∥β,其中正确的两个命题是(
)
A.①② B.①③ C.②④ D.③④
4.二面角C—BD—A为直二面角,且DA⊥平面ABC,则△ABC的形状为( )
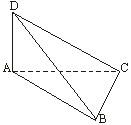
(4题图) (10题图)
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
5.线段AB的两个端点分别在直二面角α—CD—β的两个半平面内,且AB与α、β都成30°角,则异面直线AB与CD所成的角为( )
A.30° B.45° C.60° D.90°
6.如果二面角α—![]() —β的平面角是锐角,点P到α、β和棱
—β的平面角是锐角,点P到α、β和棱![]() 的距离分别为2
的距离分别为2![]() 、4、4
、4、4![]() ,则二面角大小为(
)
,则二面角大小为(
)
A.45°或30° B.15°或75° C.30°或60° D.15°或60°
7.已知直角△ABC的斜边AB在平面α内,AC、BC分别与α成30°、45°角,则α与△ABC所在平面所成二面角的度数为( )
A.30° B.45° C.60° D.60°或120°
8.异面直线a、b所成的角为![]() , a、b与平面
, a、b与平面![]() 都平行,
都平行, ![]() 平面
平面![]() ,则直线a与平面
,则直线a与平面![]() 所成的
所成的
角( )
A.与![]() 相等 B.与
相等 B.与![]() 互余
C.与
互余
C.与![]() 互补 D.与
互补 D.与![]() 不能相等
不能相等
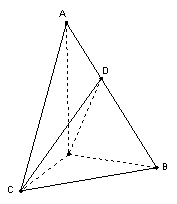
9空间四边形DABC中,![]() ,且AB=AC=
,且AB=AC=![]() ,BC=2,则二面角A—BC—D的大小为(
)
,BC=2,则二面角A—BC—D的大小为(
)
A. 300 B.
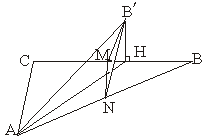
10.如图,已知∠C=90°,AC=BC,M、N分别为BC和AB中点,沿直线MN将△BMN折起,使二面角B′—MN—B为60°,则斜线B′A与平面ABC所成角的正切值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(本大题共4小题,每小题4分,共16分)
11.空间四边形ABCD中,AB=CD,且AB和CD成![]() 角,E,F分别是BC,AD的中点,则EF和AB所成的角是
。
角,E,F分别是BC,AD的中点,则EF和AB所成的角是
。
12. 矩形ABCD中,![]() ,沿对角线AC 将△
,沿对角线AC 将△![]() 折起,使
折起,使![]() 垂直,则异面直线
垂直,则异面直线![]() 间的距离等于 .
间的距离等于 .
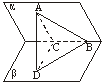
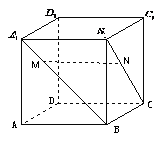 13.如图,正方体
13.如图,正方体![]() ,
,![]()
有以下四个结论:
① ![]() ②
② ![]()
③ ![]() 与面
与面![]() 成
成![]() 角; ④
角; ④ ![]() 与
与![]() 是异面直线.
是异面直线.
其中正确结论的序号是________________________________.
14. 已知线段AB的两端点到平面![]() 的距离分别是4和6,则AB的中点到平面
的距离分别是4和6,则AB的中点到平面![]() 的距离为 (注:有两种情况).
的距离为 (注:有两种情况).
三.解答题(本大题5小题,共54分)
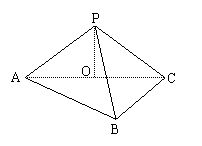
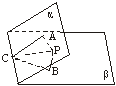
15. (本小题10分)已知二面角![]() 的大小为
的大小为![]() ,
,![]()
![]() . (1)求证:
. (1)求证:![]() ; (2)求点
; (2)求点![]() 到平面
到平面![]() 的距离。
的距离。![]()
16.(本小题10分)已知长方体![]() 中,棱
中,棱![]() 棱
棱![]() ,连结
,连结![]() ,过
,过![]() 点作
点作![]() 的垂线
的垂线
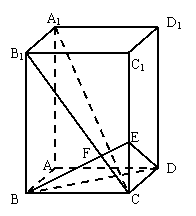 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]()
![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离;
的距离;
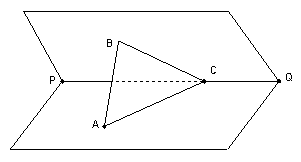
 17. (本小题10分)如图,已知P为Rt△ABC所在平面外一点,P在平面ABC上的射影O恰为斜边AC的中点,若PB=AB=1,BC=
17. (本小题10分)如图,已知P为Rt△ABC所在平面外一点,P在平面ABC上的射影O恰为斜边AC的中点,若PB=AB=1,BC=![]() ,求(1)PB与平面ABC所成的角;(2)二面角P—AB—C的正切值;
,求(1)PB与平面ABC所成的角;(2)二面角P—AB—C的正切值;
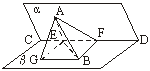
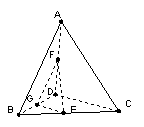
18.(本小题12分)如图,P是平面![]() 外一点,四边形
外一点,四边形![]() 是矩形,
是矩形,![]() ⊥平面
⊥平面![]() ,
,
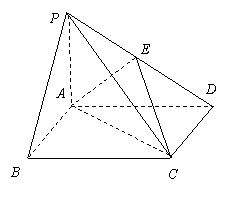
![]() ,
,![]() .
.![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 所成平面角的余弦值;
所成平面角的余弦值;
19. (本小题12分)如图,在![]() 中,
中,![]() ,斜边AB=4.
,斜边AB=4.![]() 可通过
可通过![]() 以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上。
以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上。
![]() ⑴求证:平面COD
⑴求证:平面COD ![]() 平面AOB;
平面AOB;
⑵当D为AB的中点时,求异面直线AO与CD所成角的大小;
⑶求CD与平面AOB所成角的最大值。
高2009级立体几何第三单元测试题答案
(1题图) (5题图) (1)( 6 题 图) (2)
1.如图所示,二面角α—l—β为45°,直线AB在平面α内,且与棱l成45°角.过A作AC⊥l,AD⊥平面β,垂足分别为C、D,连结CD,则CD⊥l,故∠ACD=45°,∠ABD为直线AB与平面β所成的角.
设AB=a,则在Rt△ACB中,AC=BC=![]() a.在Rt△ADC中,AD=CD=
a.在Rt△ADC中,AD=CD=![]() a.∴sinABD=
a.∴sinABD=![]() =
=![]() ,故∠ABD=30。答案:A
,故∠ABD=30。答案:A
2.法一:在PE上取一点M,作MN⊥AB于N,作NQ⊥AB交PF于Q,连结MQ.在Rt△MPN中,∠EPB=![]() ,∴MN=PN.在Rt△PQN中,∠FPB=45°,∴NQ=PN.∴MN=NQ.易证Rt△MPN≌Rt△QPN≌Rt△MNQ.
,∴MN=PN.在Rt△PQN中,∠FPB=45°,∴NQ=PN.∴MN=NQ.易证Rt△MPN≌Rt△QPN≌Rt△MNQ.
∴PM=PQ=MQ.∴∠EPF=60°.
法二:利用关系式cosEPF=cosEPB·cosFPB=cos45°·cos45°=![]() ,∴∠EPF=60°.答案:A
,∴∠EPF=60°.答案:A
3. 解析:①正确,![]() .③正确,
.③正确,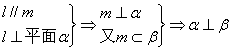 .
.
②④显然错误. 答案:B
4. 解析:过A作AE⊥BD,由题意则AE⊥面BCD,∴AE⊥BC.又DA⊥平面ABC,∴DA⊥BC.
∴BC⊥面ABD.∴BC⊥AB.∴△ABC为直角三角形.答案:B
5. 解析:如图,过A、B两点分别作棱CD的垂线AE和BF,垂足为E、F,连结EB和AF.由α—CD—β为直二面角,即α⊥β,AE⊥CD![]() AE⊥β,
AE⊥β,
∴∠ABE为AB与β所成的角.同理∠BAF为直线BA与α所成的角,即∠ABE=∠BAF=30°.过E、B分别作BF和EF的平行线,交于G点,∠ABG即为异面直线AB与CD所成的角,设AB=1,由AE=![]() =BF=EG,∠AEG=90°,故AG=
=BF=EG,∠AEG=90°,故AG=![]() .又由EF⊥AE,EF⊥EG
.又由EF⊥AE,EF⊥EG
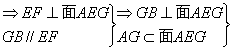
![]() GB⊥AG.即∠AGB=90°.∴sinABG=
GB⊥AG.即∠AGB=90°.∴sinABG=![]() .∴∠ABG=45°.答案:B
.∴∠ABG=45°.答案:B
6. 解析:如图,分P在二面角α—l—β内部及外部两种情况讨论.易证P、A、B、C在同一平面内,∠ACB是二面角的平面角.在Rt△APC中,sinACP=![]() =
=![]() ,∴∠ACP=30°.在Rt△BPC中,sinBCP=
,∴∠ACP=30°.在Rt△BPC中,sinBCP=![]() =
=![]() ,∴∠BCP=45°.故∠ACB=30°+45°=75°或∠ACB=45°-30°=15°.答案:B
,∴∠BCP=45°.故∠ACB=30°+45°=75°或∠ACB=45°-30°=15°.答案:B
7. 解析:作CD⊥平面α于D,作DE⊥AB于E,连结CE,则∠CED为二面角C—AB—D的平面角,设为θ,即平面α与△ABC所在平面所成二面角的度数为θ.又可知∠CAD=30°,∠CBD=45°.
设CD=x,则AC=2x,BC=![]() x,AB=
x,AB=![]() x.利用△ABC的面积公式,得CE=
x.利用△ABC的面积公式,得CE=![]() .
.
在Rt△CDE中,sin.θ= .∴θ=60°或120°.答案:D
.∴θ=60°或120°.答案:D
8. 答案:B
9. ![]()
 答案:D
答案:D
10. 解析:作B′H⊥BC于H,连结AH,则∠B′MB=60°.设B′M=a=BM,则B′H=![]() a,MH=
a,MH=![]() ,CH=
,CH=![]() a,
a,
∴AH=![]() =
=![]() a,故tanB′AH=
a,故tanB′AH=![]() =
=![]() .答案:B
.答案:B
11. 如图G是BD中点,注意![]() 或
或![]() 。所以答案是75
。所以答案是75![]() 或15
或15![]() 。
。
(11题图) (1)(12 题 图) (2)
12.如图,(1)是折前图,(2) 是折后图。![]() 同理可得
同理可得![]() ,故BD是AD与BC的公垂线段.在
,故BD是AD与BC的公垂线段.在![]() 中可得
中可得![]()
![]()
13.①③④。
14.如示意图即可理解。答案5或1.