数学单元检测----圆锥曲线
时间:90分钟 分数:120分 命题人:蠡县中学郑玉亮
一、选择题(每小题5分,共60分)
1.椭圆![]() 的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
2.过抛物线![]() 的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则
的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则![]() 等于( )
等于( )
A.10 B.
3.若直线y=kx+2与双曲线![]() 的右支交于不同的两点,则
的右支交于不同的两点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
4.(理)已知抛物线![]() 上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点( )
上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点( )
A.(2,5) B.(-2,5) C.(5,-2) D.(5,2)
(文)过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 、
、![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 等于( )
等于( )
A.4p B.5p C.6p D.8p
5.已知两点![]() ,给出下列曲线方程:①
,给出下列曲线方程:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .在曲线上存在点P满足MP=NP的所有曲线方程是( )
.在曲线上存在点P满足MP=NP的所有曲线方程是( )
(A)①③ (B)②④ (C)①②③ (D)②③④
6.已知双曲线![]() (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为![]() 、
、![]() ,点A在双曲线第一象限的图象上,若△
,点A在双曲线第一象限的图象上,若△![]() 的面积为1,且
的面积为1,且![]() ,
,![]() ,则双曲线方程为( )
,则双曲线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.圆心在抛物线![]() 上,并且与抛物线的准线及x轴都相切的圆的方程是( )
上,并且与抛物线的准线及x轴都相切的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.双曲线的虚轴长为4,离心率![]() ,
,![]() 、
、![]() 分别是它的左、右焦点,若过
分别是它的左、右焦点,若过![]() 的直线与双曲线的右支交于A、B两点,且
的直线与双曲线的右支交于A、B两点,且![]() 是
是![]() 的等差中项,则
的等差中项,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.8.
D.8.
9.(理)已知椭圆![]() (a>0)与A(2,1),B(4,3)为端点的线段没有公共点,则a的取值范围是( )
(a>0)与A(2,1),B(4,3)为端点的线段没有公共点,则a的取值范围是( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或 ![]() D.
D.![]()
(文)抛物线![]() 的焦点在x轴上,则实数m的值为( )
的焦点在x轴上,则实数m的值为( )
A.0 B.![]() C.2 D.3
C.2 D.3
10.已知双曲线中心在原点且一个焦点为![]() ,直线
,直线![]() 与其相交于
与其相交于![]() 两点,
两点, ![]() 中点横坐标为
中点横坐标为![]() ,则此双曲线的方程是(
)
,则此双曲线的方程是(
)
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
11.将抛物线![]() 绕其顶点顺时针旋转
绕其顶点顺时针旋转![]() ,则抛物线方程为( )
,则抛物线方程为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
12.若直线![]() 和⊙O∶
和⊙O∶![]() 没有交点,则过
没有交点,则过![]() 的直线与椭圆
的直线与椭圆![]() 的交点个数( )
的交点个数( )
A.至多一个 B.2个 C.1个 D.0个
二、填空题(每小题4分,共16分)
13.椭圆![]() 的离心率为
的离心率为![]() ,则a=________.
,则a=________.
14.已知直线![]() 与椭圆
与椭圆![]()
![]() 相交于A,B两点,若弦AB的中点的横坐标等于
相交于A,B两点,若弦AB的中点的横坐标等于![]() ,则双曲线
,则双曲线![]() 的两条渐近线的夹角的正切值等于________.
的两条渐近线的夹角的正切值等于________.
15.长为l![]() 0<l<1
0<l<1![]() 的线段AB的两个端点在抛物线
的线段AB的两个端点在抛物线![]() 上滑动,则线段AB中点M到x轴距离的最小值是________.
上滑动,则线段AB中点M到x轴距离的最小值是________.
16.某宇宙飞船的运行轨道是以地球中心F为焦点的椭圆,测得近地点A距离地面![]() ,远地点B距离地面
,远地点B距离地面![]() ,地球半径为
,地球半径为![]() ,关于这个椭圆有以下四种说法:
,关于这个椭圆有以下四种说法:
①焦距长为![]() ;②短轴长为
;②短轴长为![]() ;③离心率
;③离心率![]() ;④若以AB方向为x轴正方向,F为坐标原点,则与F对应的准线方程为
;④若以AB方向为x轴正方向,F为坐标原点,则与F对应的准线方程为![]() ,其中正确的序号为________.
,其中正确的序号为________.
三、解答题(共44分)
17.(本小题10分)已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线![]() 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线![]() 相交于不同的两点M、N.当
相交于不同的两点M、N.当![]() 时,求m的取值范围.
时,求m的取值范围.
18.(本小题10分)双曲线![]() 的右支上存在与右焦点和左准线等距离的点,求离心率
的右支上存在与右焦点和左准线等距离的点,求离心率![]() 的取值范围.
的取值范围.
|
(1)求证:![]() 点的坐标为
点的坐标为![]() ;
;
(2)求证:![]() ;
;
(3)求![]() 的面积的最小值.
的面积的最小值.
20.(本小题12分)已知椭圆方程为![]() ,射线
,射线![]() (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(1)求证直线AB的斜率为定值;
(2)求△![]() 面积的最大值.
面积的最大值.
圆锥曲线单元检测答案
1. A 2.B 3 D 4 理C 文A 5 D
13.![]() 或
或![]() 14.
14.![]() 15.
15.![]() 16.①③④
16.①③④
17.(1)依题意可设椭圆方程为 ![]() ,则右焦点F(
,则右焦点F(![]() )由题设
)由题设
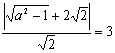 解得
解得![]() 故所求椭圆的方程为
故所求椭圆的方程为![]() .
.
![]() ………………………………………………4分.
………………………………………………4分.
(2)设P为弦MN的中点,由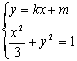 得
得 ![]()
由于直线与椭圆有两个交点,![]() 即
即 ![]() ①………………6分
①………………6分
![]() 从而
从而![]()
![]() 又
又![]() ,则
,则
![]() 即
即 ![]() ②…………………………8分
②…………………………8分
把②代入①得 ![]() 解得
解得 ![]() 由②得
由②得 ![]() 解得
解得![]() .故所求m的取范围是(
.故所求m的取范围是(![]() )……………………………………10分
)……………………………………10分
18.设M![]() 是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离
是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离![]() ,即
,即![]() ,由双曲线定义可知
,由双曲线定义可知 ![]() ……5分
……5分
由焦点半径公式得
![]()
![]() …………………………7分
…………………………7分
而![]() 即
即 ![]() 解得
解得![]() 但
但 ![]() ……………………………………10分
……………………………………10分
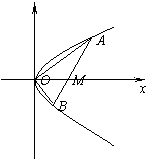
19. (1
) 设![]() 点的坐标为
点的坐标为![]() , 直线
, 直线![]() 方程为
方程为![]() , 代入
, 代入![]() 得
得
![]() ①
① ![]() 是此方程的两根,
是此方程的两根,
∴![]() ,即
,即![]() 点的坐标为(1, 0).
点的坐标为(1, 0).
(2 ) ∵ ![]()
∴ ![]()
∴ ![]() .
.
(3)由方程①,![]() ,
, ![]() , 且
, 且 ![]() ,
,
于是![]()
![]() =
=![]() ≥1,
≥1,
∴ 当![]() 时,
时,![]() 的面积取最小值1.
的面积取最小值1.
20.解析:(1)∵ 斜率k存在,不妨设k>0,求出![]() (
(![]() ,2).直线MA方程为
,2).直线MA方程为![]() ,直线
,直线![]() 方程为
方程为![]() .
.
分别与椭圆方程联立,可解出![]() ,
,![]() .
.
∴ ![]() . ∴
. ∴ ![]() (定值).
(定值).
(2)设直线![]() 方程为
方程为![]() ,与
,与![]() 联立,消去
联立,消去![]() 得
得![]()
![]() .
.
由![]() 得
得![]() ,且
,且![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() .
.
设![]() 的面积为
的面积为![]() .
.
∴ ![]() .
.
当![]() 时,得
时,得![]() .
.
圆锥曲线课堂小测
时间:45分钟 分数:60分 命题人:郑玉亮
一、选择题(每小题4分共24分)
1.![]() 是方程
是方程 ![]() 表示椭圆或双曲线的 ( )
表示椭圆或双曲线的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
2.与曲线![]() 共焦点,而与曲线
共焦点,而与曲线![]() 共渐近线的双曲线方程为 ( )
共渐近线的双曲线方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.我国发射的“神舟3号”宇宙飞船的运行轨道是以地球的中心![]() 为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为( )
为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为( )
A.![]() B.
B.![]()
C.mn D.2mn
4.若椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点F1、F2,P是两曲线的一个交点,则
有相同的焦点F1、F2,P是两曲线的一个交点,则![]() 的面积是 ( )
的面积是 ( )
A.4 B.![]()
5.圆心在抛物线![]() 上,且与
上,且与![]() 轴和该抛物线的准线都相切的一个圆的方程是( )
轴和该抛物线的准线都相切的一个圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.已知双曲线![]() 的离心率
的离心率![]() ,
,![]() .双曲线的两条渐近线构成的角中,以实轴为角平分线的角记为
.双曲线的两条渐近线构成的角中,以实轴为角平分线的角记为![]() ,则
,则![]() 的取值范围是( ).
的取值范围是( ).
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
![]()
二、填空题(每小题4分共16分)
7.若圆锥曲线![]() 的焦距与
的焦距与![]() 无关,则它的焦点坐标是__________.
无关,则它的焦点坐标是__________.
8.过抛物线![]() 的焦点作直线与此抛物线交于P,Q两点,那么线段PQ中点的轨迹方
的焦点作直线与此抛物线交于P,Q两点,那么线段PQ中点的轨迹方
程是 .
9.连结双曲线![]() 与
与![]() (a>0,b>0)的四个顶点的四边形面积为
(a>0,b>0)的四个顶点的四边形面积为![]() ,
,
连结四个焦点的四边形的面积为![]() ,则
,则![]() 的最大值是________.
的最大值是________.
10.对于椭圆![]() 和双曲线
和双曲线![]() 有下列命题:
有下列命题:
①椭圆的焦点恰好是双曲线的顶点;
②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点;
④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是 .
三、解答题(20分)
11.(本小题满分10分)已知直线![]() 与圆
与圆![]() 相切于点T,且与双曲线
相切于点T,且与双曲线![]() 相交于A、B两点.若T是线段AB的中点,求直线
相交于A、B两点.若T是线段AB的中点,求直线![]() 的方程.
的方程.
12.(10分)已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
(1)求椭圆的方程.
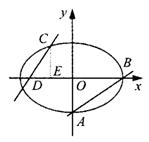 (2)已知定点
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
圆锥曲线课堂小测答案
1 B
![]() )8.
)8.![]() 9.
9.![]() 10.①②
10.①②
11.解:直线![]() 与
与![]() 轴不平行,设
轴不平行,设![]() 的方程为
的方程为 ![]() 代入双曲线方程 整理得
代入双曲线方程 整理得
![]() ……………………3分 而
……………………3分 而![]()
![]() ,于是
,于是
![]() 从而
从而![]() 即
即 ![]() ……5分
……5分
![]() 点T在圆上
点T在圆上 ![]() 即
即![]() ①
①
由圆心![]() .
.![]() 得
得 ![]() 则
则 ![]() 或
或 ![]()
当![]() 时,由①得
时,由①得 ![]() 的方程为
的方程为 ![]() ;
;
当![]() 时,由①得
时,由①得 ![]()
![]() 的方程为
的方程为![]() .故所求直线
.故所求直线![]() 的方程为
的方程为![]() 或
或 ![]() …………………………10分
…………………………10分
12.解:(1)直线AB方程为:![]() .
.
依题意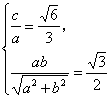 解得
解得 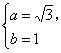
∴ 椭圆方程为 ![]() .
.
(2)假若存在这样的k值,由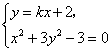 得
得![]()
![]() .
.
∴ ![]() . ①
. ①
设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则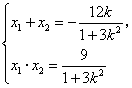 ②
②
而![]() .
.
要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE时,则![]() ,即
,即![]() .
.
∴ ![]() . ③
. ③
将②式代入③整理解得![]() .经验证,
.经验证,![]() ,使①成立.
,使①成立.
综上可知,存在![]() ,使得以CD为直径的圆过点E.
,使得以CD为直径的圆过点E.