2004-2005学年度上学期
高中学生学科素质训练
高二数学期中测试题
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
一、选择题(本大题共12小题,每小题5分,共60分)
1.如果a、b是满足不等式ab<0的实数,那么 ( )
A.a+b>a-b B.a+b<a-b C.a-b<a-b D. a-b<a+b
2.已知c<0,在下列不等式中成立的一个是 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
3.下列各式中,最小值为2的是 ( )
A.![]() B.
B.![]() C.tanx+cotx D.
C.tanx+cotx D. ![]()
4.不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若直线(a+2)x+(a+3)y-5 =0与直线6x+(2a-1)y-7=0互相垂直,则a的值为 ( )
A.1 B.![]() C.-1或
C.-1或![]() D.
D.![]() 或1
或1
6.当点(x ,y)在直线x+3y=2上移动时, z =3x +27y+3的最小值是 ( )
B.![]() B.
B.![]() C.0 D.9
C.0 D.9
7.曲线y2=4x关于直线x=2对称的曲线方程是 ( )
A.y2=8-4x B.y2=4x-8 C.y2=16-4x D.y2=4x-16
8.A点关于8x+6y=25的对称点恰为原点,则A点的坐标为 ( )
A.(2,
![]() )
B.
)
B.![]() C.(3,
4) D.(4,
3)
C.(3,
4) D.(4,
3)
9.已知x2+y 2 = 1 ,若x + y -k ≥0对符合条件一切x 、y都成立,则实数k的最大值为( )
A.![]() B.-
B.-![]() C.0 D.1
C.0 D.1
10.已知A(2,-3) 、B(-3,-2),直线![]() 过P(1,1)且与线段AB有交点,设直线
过P(1,1)且与线段AB有交点,设直线![]() 的斜率为k,则k的取值范围是
( )
的斜率为k,则k的取值范围是
( )
A.k≥![]() 或k≤-4 B.-4≤k≤
或k≤-4 B.-4≤k≤![]() C.k≥
C.k≥![]() 或k≤
或k≤![]() D.
D.![]() ≤k≤4
≤k≤4
二、填空题(本大题共4小题,每小题4分,共16分)
11.不等式![]() 的解集是____________________________.
的解集是____________________________.
12.不论m为何实数,直线(m-1)x-y+2m+1=0恒过定点_______________.
13.与直线3x+4y-7=0垂直,且与原点的距离为6的直线方程为 .
14.有下列命题:
(1)若两条直线平行,则其斜率必相等;
(2)若两条直线的斜率乘积为-1, 则其必互相垂直;
(3)过点(-1,1),且斜率为2的直线方程是![]() ;
;
(4)同垂直于x轴的两条直线一定都和y轴平行;(5) 若直线的倾斜角为![]() ,则
,则![]() .
.
其中为真命题的有_____________(填写序号).
三、解答题(本大题共6小题,共74分)
15.解关于x的不等式![]() (12分)
(12分)
16.已知P是直线![]() 上一点,将直线
上一点,将直线![]() 绕P点逆时针方向旋转
绕P点逆时针方向旋转![]() (
(![]() )所得直线为
)所得直线为![]() :
:![]() .若继续绕P点逆时针方向旋转
.若继续绕P点逆时针方向旋转![]() 角,得直线
角,得直线![]() :
:![]() .求直线
.求直线![]() 的方程.(12分)
的方程.(12分)
17.已知![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(1)比较![]() 与
与![]() 的大小;
的大小;
(2)设![]() ,
,![]() ,求证:
,求证:![]() .(12分)
.(12分)
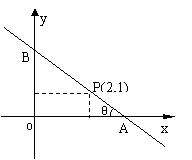
18.过点P(2,1)作直线![]() 交x、y正半轴于A、B两点,当
交x、y正半轴于A、B两点,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.(12分)
的方程.(12分)
19.某段城际铁路线上依次有A、B、C三站,AB=5km,BC=3km,在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度![]() 匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(1)分别写出列车在B、C两站的运行误差;
(2)若要求列车在B,C两站的运行误差之和不超过2分钟,求![]() 的取值范围.(14分)
的取值范围.(14分)
20.在平面直角坐标系中,设矩形OPQR的顶点按逆时针顺序依次为O(0,0),P(1,t) Q(1-2t,2+t),R(-2t,2)其中t![]() (0,+∞),
(0,+∞),
(1)求矩形OPQR在第一象限部分的面积S(t);
(2)求S(t)的最小值.(14分)
参考答案
一、选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | D | B | C | D | C | D | B | A |
二、填空题(本大题共4小题,每小题6分,共24分)
11.![]() 12.
12.![]() 13.
13.![]() 14. (2)
14. (2)
三、解答题(本大题共6题,共76分)
15.(12分)[解析]:原不等式![]()
![]() . 分情况讨论
. 分情况讨论
(i)当a<0或a>1时,有a<a2,此时不等式的解集为![]() ;
;
(ii)当![]() 时,有a2<a,此时不等式组的解集为
时,有a2<a,此时不等式组的解集为![]()
(iii)当a=0或a=1时,原不等式无解.
综上,当a<0或a>1时时,原不等式的解集为;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]()
当a=0或a=1时,原不等式的解集为φ.
![]() 16.(12分)[解析]:由题意知点P是
16.(12分)[解析]:由题意知点P是![]() 与
与![]() 的交点,且
的交点,且![]() ,则由
,则由 ![]()
![]()
![]()
![]() ,即P(7,-1),又
,即P(7,-1),又![]() ,所以直线
,所以直线![]() 的方程为:
的方程为:![]()
即![]() .
.
17.(12分)
[解析]:.(1)![]()
![]()
即 ![]() .
.
(2)由(1)![]()
![]() =
=![]()
![]()
![]()
![]() . 得证.
. 得证.
18.(12分)
[解析]: 设![]() :
:![]() (如图)
(如图)
则![]()
![]()
又P(2,1)在![]() 上,
上,
![]()
![]()
设![]() ,则
,则![]() 等号当其仅当
等号当其仅当![]() 时成立,这时a=b=3.
时成立,这时a=b=3.
![]() .
.
19.(14分)
[解析]:(1)列车在B,C两站的运行误差(单位:分钟)分别是 ![]() 和
和![]() .
.
(2)由于列车在B,C两站的运行误差之和不超过2分钟,所以![]() (*)
(*)
当![]() 时,(*)式变形为
时,(*)式变形为![]() , 解得
, 解得![]()
当![]() 时,(*)式变形为
时,(*)式变形为![]() , 解得
, 解得![]()
当![]() 时,(*)式变形为
时,(*)式变形为![]() , 解得
, 解得![]()
综上所述,![]() 的取值范围是[39,
的取值范围是[39,![]() ].
].
20.(14分)[解析]:![]() ,
,![]()
(1)当RQ与y轴交与点S,即![]() 设S(0,m),
设S(0,m),
![]() ,
,![]() ,
,
![]()
![]() ;
;
当PQ与y轴交与点S,即![]() 设S(0,n),
设S(0,n),![]() ,
,
![]() ,
,![]() .
.
![]() 综上知:S(t)=
综上知:S(t)= 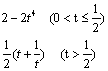 .
.
(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,这时t=1.
,这时t=1.
![]() 的最小值为1.
的最小值为1.