高二文科数学第二学期期末调研试卷
高二数学(文科)
本试卷共4页，20小题，满分150分．考试用时120分钟．
注意事项：
1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自已的姓名、班别、学号、试室号填写在答题卡上．
2．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上．
参考公式及数据：
用最小二乘法求线性回归方程系数公式：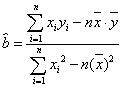
，
．
随机变量
的临界值表:
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
１．在两个变量的回归分析中，作散点图是为了（ ）
Ａ．直接求出回归直线方程 Ｂ．直接求出回归方程
Ｃ．根据经验选定回归方程的类型 Ｄ．估计回归方程的参数
2． 将圆
变换为椭圆
的伸缩变换公式为（ ）
A． 
B． 
C． 
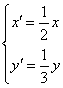D．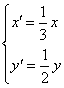 
3．
＝（ ）
A．2ｉ B．-2ｉ C．-ｉ D．ｉ
4. 点
的极坐标是
，则点的直角坐标为（ ）
A．
B．
C．
D．
5. 若
则复数
表示的点在第 ( ) 象限.
A．一 B．二 C．三 D．四
6. 由数列1，3，6，10，……猜测该数列的第n项可能是（ ）
A．
B．
C．
D．
7. 与方程xy=1表示同一曲线的参数方程(其中t为参数)是（ ）
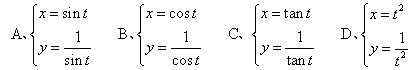
8. 直线：3x-4y-9=0与圆：
(θ为参数)的位置关系是( )
A．相切 B．相离 C．相交但直线不过圆心 D．直线过圆心
9．极坐标方程
、
表示的曲线分别是（ ）
A．直线、直线 B．圆、直线
C．直线、圆 D．圆、圆
10．如图，圆周上按顺时针方向标有1，2，3，4，5五个点。
一只青蛙按顺时针方向绕圆从一点跳到另一点。若它停在
奇数点上，则下一次只能跳一个点；若停在偶数点上，则跳
两个点。该蛙从5这点跳起，经2008次跳后它将停在的点是 ( )
A．
B．
C．
D．
二、填空题：本大题共4小题，每题5分，共20分.
11．在复平面内，O是原点，向量
对应的复数
，则
为
。
12．某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：
| 性别 专业 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
为了判断主修统计专业是否与性别有关系，根据表中的数据，得到
，那么可以判定主修统计专业与性别有关系，这种判断出错的可能性为 。
13.在平面直角坐标系xOy 中，圆C的参数方程为
（参数
），则圆C的圆心坐标为_______.
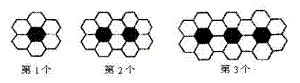
14．黑白两种颜色的正六形地面砖块按如图的规 律拼成若干个图案，则第五个图案中有白色地面砖 块.
三、解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.
15．（本小题满分12分）
实数m取什么值时，复数
（1）实数？（2）虚数？（3）纯虚数？
16．（本小题满分12分）
求证：
。
17．（本小题满分14分）
某种产品的广告费支出x与销售额y(单位：百万元)之间有如下的对应数据：
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
=
x+
；
（3）要使这种产品的销售额突破一亿元(含一亿元)，则广告费支出至少为多少百万元？
（结果精确到0.1，参考数据：2×30＋4×40＋5×50＋6×60＋8×70=1390。）
 |
18. （本小题满分
分）
已知A,B两点是椭圆
与坐标轴正半轴的
两个交点,
(1) 求
的面积
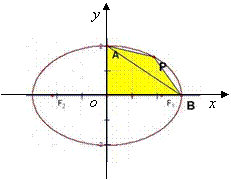
(2) 在第一象限的椭圆弧上求一点P,
使四边形OAPB的面积最大.
19．（本小题满分分）
已知函数
，
（1）求
的单调区间； （2）求在
上的最大值和最小值。
20．（本小题满分分）
对任意函数，
，可按如图所示，构造一个数列发生器，其工作原理如下：
① 输入数据
，经数列发生器输出
；
② 若
，则数列发生器结束工作；若
，将
反馈回输入端，再输出
，并依此规律进行下去。
现定义
。
（1）若输入
，则由数列发生器产生数列
，
写出数列的所有项；
（2）若要数列发生器产生一个无穷的常数列，试求
输入的初始数据
的值。
（3）若输入时，产生的无穷数列满足：
对任意正整数
，均有
，求的取值范围。
附加题（本题为附加题，如果解答正确，加5 分，但全卷总分不超过150分）
设
是由非负整数组成的数列，且满足
，
，
，
（1）求
；并猜
的关系(
,不证明);.
（2）求的通项公式。
高二数学(文科)参考答案及评分标准
一、选择题：
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | D | C | D | B | C | C | B | A |
二、填空题： 11．
12．5% 13．（0，2） 14．22；
三、解答题：
15．【解】
（1）当
, …………………………1分
即
或
时，………………… 3分
z是实数；……………………………… 4分
（2）当
，……………………… 5分
即
且
时，………………… 7分
z是虚数； ………………………………8分
（3）当
……………11分
即m=2时z是纯数。……………………12分
16．【证明】
因为
和
都是正数，………1分
所以为了证明 ……………3分
只需证
……………5分
只需证
……………8分
即证明
……………9分
即证明
……………10分
即证明
……………11分
因为21<25显然成立，所以原不等式成立. ……………12分
17．【解】（1）散点图如下图所示：
（2）
，
，
，
………6分
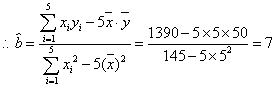， ………8分
，
所求回归直线方程为
（3）依题意，有
所以广告费支出至少为12.1百万元.
…………………14分
18．【解】(1) 面积
，………………………………3分
(2)设点
，
，
即
， …………………………5分
要使
最大，只需
最大即可，
从而点P到直线AB的距离d最大， ……………………………6分
直线AB的方程为
即
…………………………8分
，……………………10分
，
当
时，d取得最大值， ……………………12分
此时四边形OAPB的面积最大，点P的坐标为
。…………14分
19．【解】（1）因为，所以
……………………2分
由
得
或
,
……………………4分
故函数的单调递增区间为（-∞，-），（2，+∞）；
…………6分
由
得
……………………8分
故函数的单调递减区间为（
，2） ……………………9分
（2）令
得
……………………10分
由（1）可知，在上有极小值
，…………11分
而
，
，因为
……………………13分
所以在上的最大值为4，最小值为
。…………14分
20．【解】（1）函数的定义域为
，
所以数列只有3项：
。………………3分
（2）令
，即
，
解得
或
，
即当
或
时，
，
故当时，得到常数列
；
当时，得到常数列
。 …………………………8分
（3）解不等式
得
或
，
要使
，则
或
，
………………………10分
对于函数
，
若，则
，
，………………………12分
当时，
，且
，依次类推，
可得数列的所有项均满足
，
综上所述，
；由，得
。 …………………14分
附加题（本题为附加题，如果解答正确，加5 分，但全卷总分不超过150分）
【解】
（1）由于题设有
，且
都是非负整数，于是的取值只能是1，2，5，10。
若
，则
，这与
为非负整数矛盾；
若
，则
，这与为非负整数矛盾；
若
，则
，这也与为非负整数矛盾；
所以
。
；猜想： 
，。…………2分
（2）
，，，，
，
，
即
………………………………5分