班级_______班 高二理科数学8月底月考试题
考号_____________ (测试内容 :必修五第一章:解三角形和第二章:数列 命题:方锦昌)
姓名__________ 特别提示:本卷中有多处要用到均值不等式,即a2+b2≥2ab当且仅当a=b时等号成立)
一、 选择题(5×10=50分):
1、若lga、lgb、lgc成等差数列,则有( )
A、b=![]() B、b=
B、b=![]() (lga+lgc) C、 a、b、c成等比数列 D、a、b、c成等差数列
(lga+lgc) C、 a、b、c成等比数列 D、a、b、c成等差数列
2、已知△ABC中,a=4,b=4![]() ,∠A=30°,则∠B等于( )
,∠A=30°,则∠B等于( )
A.30° B.30°或150° C.60° D.60°或120°
3、![]() 的三角A、B、C所对的边a、b、c成等比数列,则∠B的取值范围是( )
的三角A、B、C所对的边a、b、c成等比数列,则∠B的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、设![]() 是公差为正数的等差数列,若
是公差为正数的等差数列,若![]() ,
,![]() ,则
,则![]() ( ) A.
( ) A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、若数列![]() 中,
中,![]() = 43-3n,则
= 43-3n,则![]() 最大值n=
( )
最大值n=
( )
A.13
B.
6、某种细菌在培养过程中,每20分钟分裂一次(一个分裂二个)经过3小时,这种细菌由1个可以繁殖成( )A.511个 B.512个 C.1023个 D.1024个
7、⊿ABC为钝角三角形,a=3,b=4,c=x,C为钝角,则x的取值范围为( )
A
5<x<7
B x<
8、已知¦(n)= 1+ + + +…+ 则¦(n+1)- ¦(n)之值为( )
A B C + D + +
9、已知△ABC中,sinA∶sinB∶sinC=k∶(k+1)∶2k (k≠0),则k的取值范围为( )
A.(2,+∞) B.(-∞,0) C.(-![]() ,0) D.(
,0) D.(![]() ,+∞)
,+∞)
10、已知方程![]() 的四个根组成一个首项为
的四个根组成一个首项为![]() 的等差数列,则
的等差数列,则![]() ( )A、1
B、
( )A、1
B、![]() C、
C、![]() D、
D、![]()
二、填空题(5×5=25分):
11、数列![]() 的前n项的和Sn=2n2-n+1,则an=
的前n项的和Sn=2n2-n+1,则an=
12、等比数列![]() 的各项均为正数,且
的各项均为正数,且![]() ,则
,则![]() 。13、在数列{an}中,若a1=1,an+1=2an+3
(n≥1),则该数列的通项an=_______ .__.
。13、在数列{an}中,若a1=1,an+1=2an+3
(n≥1),则该数列的通项an=_______ .__.
14、在△ABC中,若sinAsinB=cos2![]() ,则△ABC为_____ 三角形(填锐角、直角或钝角)
,则△ABC为_____ 三角形(填锐角、直角或钝角)
15、数列 1![]() , 2
, 2![]() , 3
, 3![]() , 4
, 4![]() , 5
, 5![]() , …, 的前n项之和等于 .
, …, 的前n项之和等于 .
三、解答题(共75分)
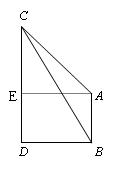 16(12分).如图,在一建筑物底部B处和顶部A 处分别测得山顶C处的仰角为
16(12分).如图,在一建筑物底部B处和顶部A 处分别测得山顶C处的仰角为![]() 和
和![]() (AB连线垂直于水平线),已知建筑物高AB=
(AB连线垂直于水平线),已知建筑物高AB=
17(12分)、已知数列![]() 是等差数列,
是等差数列,![]() 是等比数列,且
是等比数列,且![]()
![]() ,
, ![]() ,(I)求数列
,(I)求数列![]() 的通项公式;(II)求数列
的通项公式;(II)求数列![]() 的前10项和
的前10项和![]() 。
。
18(12分)、已知![]() 、
、![]() 、
、![]() 分别是
分别是![]() 的三个内角
的三个内角![]() 、
、![]() 、
、![]() 所对的边;(1)若
所对的边;(1)若![]() 面积
面积![]() 求
求![]() 、
、![]() 的值;(2)若
的值;(2)若![]() ,且
,且![]() ,试判断
,试判断![]() 的形状.
的形状.
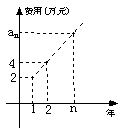 19(12分)、某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用
19(12分)、某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图。
的信息如下图。
(1)求![]() ;(2)引进这种设备后,第几年后该公司开始获利;
;(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
20(13分)、已知![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() (n=1,2,3…).令
(n=1,2,3…).令![]() (n=1,2,3…).(Ⅰ)求证: 数列
(n=1,2,3…).(Ⅰ)求证: 数列![]() 为等比数列;(Ⅱ)令
为等比数列;(Ⅱ)令![]() ,记
,记![]() ,比较
,比较![]() 与
与![]() 的大小。
的大小。
21(14分)、已知数列![]() 满足
满足![]()
![]() ,且
,且![]() ,
,![]() .
.
⑴求数列的前三项![]() ,
,![]() ,
,![]() ;⑵数列
;⑵数列![]() 为等差数列,求实数
为等差数列,求实数![]() 的值;⑶求数列
的值;⑶求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
1、 C ;2、 D ;3、A ; 4、B ;5、B ;6、B ;7、A;8、D ;9、D;10、C
11、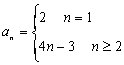 ;12、9;13、
;12、9;13、![]() ;14、直角三角形;15、
;14、直角三角形;15、![]()
16(12分)解:如图,在![]() 中,由正弦定理可得
中,由正弦定理可得
![]() 即
即 ![]()
所以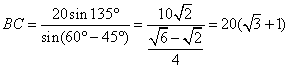 在
在![]() 中,
中,![]() 所以山高为
所以山高为![]() 米
米
17(12分)、(I)![]() 是等比数列,且
是等比数列,且![]() ,
, ![]()
![]()
![]()
![]() (II)
(II)![]() 数列
数列![]() 是等差数列,
是等差数列,![]() ,
又
,
又![]()
![]()
![]()
![]()
![]() 从而
从而![]() …9分
…9分 ![]()
![]()
![]()
![]()
18(12分)、(1)![]() ,
,![]() ,得
,得![]() 由
由![]() ,∴
,∴![]()
(2)由![]() ,所以
,所以![]() 在
在![]() 中,
中,![]() ,所以
,所以![]() 所以
所以![]() 是等腰直角三角形
是等腰直角三角形
19(12分)、解:(1)由题意知,每年的费用是以2为首项,2为公差的等差数列,求得: ![]() (2)设纯收入与年数n的关系为f(n),则: f(n)=21n-[2n+
(2)设纯收入与年数n的关系为f(n),则: f(n)=21n-[2n+![]() ]-25=20n-n2-25由f(n)>0得n2-20n+25<0
解得
]-25=20n-n2-25由f(n)>0得n2-20n+25<0
解得![]() 又因为n
又因为n![]() ,所以n=2,3,4,……18.即从第2年该公司开始获利
,所以n=2,3,4,……18.即从第2年该公司开始获利
(2)年平均收入为![]() =20-
=20-![]() 当且仅当n=5时,年平均收益最大.所以这种设备使用5年,该公司的年平均获利最大。
当且仅当n=5时,年平均收益最大.所以这种设备使用5年,该公司的年平均获利最大。
20(13分)、(Ⅰ)解:![]()
![]() ,
, ![]() .
. ![]() ∴
∴![]() 是以2为公比的等比数列 (Ⅱ)
是以2为公比的等比数列 (Ⅱ)![]() ,
,![]()
![]() .
.![]() .
.
![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() ×
×![]() +
+ ![]() ×
×![]() ×
× ![]() +…+
+…+![]() ×
×![]() ×
×![]() =
= ![]() ×(
×(![]() -
-![]() ) +
) +![]() ×(
×(![]() -
-![]() ) +…+
) +…+![]() ×(
×(![]() -
-![]() ) =
) = ![]() ×(
×(![]() -
-![]() ) =
) = ![]() -
-![]()
![]()
21(14分)、解、⑴、由![]()
![]() ,且
,且![]() 得
得![]() ,得
,得![]() 同理,得
同理,得![]() ,
,![]() ⑵、 对于
⑵、 对于![]() ,且
,且![]() ,
,
∵![]() 又数列
又数列![]() 为等差数列,∴
为等差数列,∴ ![]() 是与
是与![]() 无关的常数,∴
无关的常数,∴ ![]() ,
,![]() ⑶、 由⑵知,等差数列
⑶、 由⑵知,等差数列![]() 的公差为1, ∴
的公差为1, ∴ ![]() ,得
,得![]() . ∴
. ∴ ![]()
![]() , 记
, 记![]() ,则有
,则有 ![]() , 两式相减,得
, 两式相减,得 ![]() , 故
, 故 ![]() .
.