高二理科数学下学期期末试题
2008.6
注意:本试卷满分150分,分为Ⅰ卷和Ⅱ卷两部分,第Ⅰ卷的答案涂在答题卡上,第Ⅱ卷的答案按要求写在答题纸上.
Ⅰ卷(满分50分)
一、选择题:本题共10个小题,每小题5分,共50分,每题只有一个正确答案,答案涂在答题卡上.
1. 已知α、β是两个不重合的平面,l、m是两条不重合的直线,则α∥β的一个充分条件是 ( )
A.l⊥α,m⊥β且l∥ m
B.l![]() α,m
α,m![]() β且l∥m
β且l∥m
C.l![]() α,m
α,m![]() β且l∥β、m∥β
D.l∥α,m∥β且l∥ m
β且l∥β、m∥β
D.l∥α,m∥β且l∥ m
2. 集合![]() 中元素个数为( )
中元素个数为( )
A.2个 B.3个 C.4个 D.5个
3. 若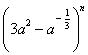 的展开式中含有常数项,则正整数n的最小值是( )
的展开式中含有常数项,则正整数n的最小值是( )
A.5
B
4. 将7名学生分配到甲、乙两个宿舍,每个宿舍至少安排2名学生,那么互不相同的安排方法的种数为( )
A.252
B.
5. 一个盒子装有11只球,球上分别标有号码1,2,3,…,11,若随机取出6只球,它们号码之和是奇数的概率是( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
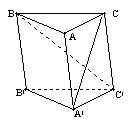 6. 如图,在斜三棱柱
6. 如图,在斜三棱柱![]() 中,
中,![]() ,则
,则![]() 在平面
在平面![]() 上的射影
上的射影![]() 必在( )
必在( )
A、![]() 内部 B、直线
内部 B、直线![]() 上
上
C、直线![]() 上 D、直线
上 D、直线![]() 上
上
7.已知函数![]() 在点
在点![]() 处存在极限,且
处存在极限,且![]() ,
,![]() ,则函数
,则函数![]() 在点
在点![]() 处的极限为( )
处的极限为( )
A.-1或3 B.-1 C.7 D.-1或7
8.如果![]() ∥
∥![]() ,AB与AC是夹在平面
,AB与AC是夹在平面![]() 与
与![]() 之间的两条线段,
之间的两条线段,![]() 且
且![]() ,直线AB与平面
,直线AB与平面![]() 所成的角为
所成的角为![]() ,那么线段AC长的取值范围是( )
,那么线段AC长的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9. 如果随机变量![]() ,则P
,则P![]() 等于( )
等于( )
A. 2Φ(1)-1 B. Φ(4)-Φ(2)
C. Φ(2)-Φ(4) D. Φ(-4)-Φ(-2)
10. 2003年春季,我国部分地区![]() 流行,党和政府采取果断措施,防治结合,很快使病情得到控制.下表是某同学记载的5月1日至5月12日每天北京市
流行,党和政府采取果断措施,防治结合,很快使病情得到控制.下表是某同学记载的5月1日至5月12日每天北京市![]() 病患者治愈者数据,及根据这些数据绘制出的散点图.
病患者治愈者数据,及根据这些数据绘制出的散点图.
| 日期 | 5.1 | 5.2 | 5.3 | 5.4 | 5.5 | 5.6 | ||
| 人数 | 100 | 109 | 115 | 118 | 121 | 134 | ||
| 日期 | 5.7 | 5.8 | 5.9 | 5.10 | 5.11 | 5.12 | ||
|
| 141 | 152 | 168 | 175 | 186 | 203 |
下列说法:
①根据此散点图,可以判断日期与人数具有线性相关关系;
②若日期与人数具有线性相关关系,则相关系数![]() 与临界值
与临界值![]() 应满足
应满足![]() ; ③根据此散点图,可以判断日期与人数具有一次函数关系. 其中正确的个数为( )
; ③根据此散点图,可以判断日期与人数具有一次函数关系. 其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
Ⅱ卷(满分100分)
二、填空题 (本大题共4小题,每小题4分共16分)
11. 若![]() 能被25整除,则a的最小正数值是___________ .
能被25整除,则a的最小正数值是___________ .
12.设常数![]() ,
,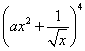 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则![]() __
__
__
__
13. 某种产品有3只次品和6只正品,每次取出一只测试,直到3只次品全部测出为止,求第三只次品在第6次测试时被发现的不同的测试情况有_________种.
 14.已知函数
14.已知函数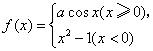 在点
在点![]() 处连续,则
处连续,则![]()
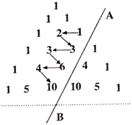
15.如图所示,在杨辉三角中,斜线AB上方箭头所示的
数组成一个锯齿形的数列:1,2,3,3,6,4,10,……,记
这个数列前n项的和为S(n),则S(16)等于 .
三、解答题:(本大题共6小题,满分75分,解答应写出文字说明,证明过程或演算步骤)
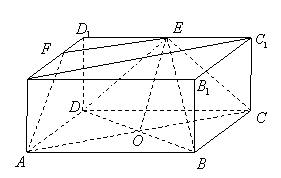
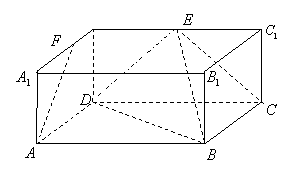 16.(本小题满分12分)如图,在长方体
16.(本小题满分12分)如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() .
.
17.(本小题满分12分)已知10件产品中有3件是次品.
(1)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(2)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
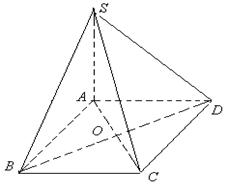
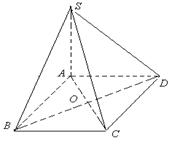 18. (本小题满分12分)已知四棱锥
18. (本小题满分12分)已知四棱锥![]() 的底面
的底面![]() 是正方形,侧棱
是正方形,侧棱![]() 的中点
的中点![]() 在底面上的射影正好落在底面正方形的中心
在底面上的射影正好落在底面正方形的中心![]() 点,而点
点,而点![]() 在截面
在截面![]() 上的射影正好是
上的射影正好是![]() 的重心.
的重心.
(I)求![]() 与底面
与底面![]() 所成角的正切值;
所成角的正切值;
(II)
求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
19.(本小题满分12分)现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为![]() 、
、![]() 、
、![]() ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是![]() ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为![]() ,对乙项目每投资十万元,
,对乙项目每投资十万元, ![]() 取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量![]() 、
、![]() 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求![]() 、
、![]() 的概率分布和数学期望
的概率分布和数学期望![]() 、
、![]() ;
;
(II) 当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
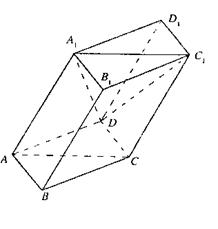
|
∠ABC=60°,平面AA
(1)证明:BD⊥AA1;
(2)求二面角D—A
(3)在直线CC1上是否存在点P,使BP//平面DA
若存在,求出点P的位置;若不存在,说明理由.
21.(本小题满分14分)已知不等式![]() ,其中
,其中![]() 为大于2的整数,
为大于2的整数,![]() 表示不超过
表示不超过![]() 的最大整数. 设数列
的最大整数. 设数列![]() 的各项为正,且满足
的各项为正,且满足![]()
(Ⅰ)证明:![]()
(Ⅱ)猜测数列![]() 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当![]() 时,对任意b>0,都有
时,对任意b>0,都有![]() .
.
高二数学试题答题卡
姓名: 得分:
一.选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二.填空题(本大题共5小题,每小题5分,共25分)
11. 12.
13. 14. 15.
 三.解答题(本大题共6小题,共75分)
三.解答题(本大题共6小题,共75分)
16.(本题满分12分)
17. (本题满分12分)
18.(本题满分12分)
19.(本题满分12分)
20.(本题满分13分)
21.(本题满分14分)
08年高二下学期期末考试
参考答案
一、选择题:(本大题共10个小题;每小题5分,共50分.)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | A | C | C | B | A | D | C | D | B | C |
二、填空题:(本大题共5小题,每小题5分,共25分.)
11、4; 12、1; 13、7200; 14 、 -1 ; 15、 164;
三、解答题:(本大题共6小题,共75分.)
16、证明:![]() 侧面
侧面![]() ,
,![]() 侧面
侧面![]() ,
,
![]() ,………3分
,………3分
在![]() 中,
中,![]() ,则有
,则有![]() ,
,
![]() ,
,![]() ,
,
又![]()
![]() 平面
平面![]() . …………6分
. …………6分
 (2)证明:连
(2)证明:连![]() 、
、![]() ,连
,连![]() 交
交![]() 于
于![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边
是平行四边
![]() ………10分
………10分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() . ……12分
. ……12分
17、解:(1)任意取出3件产品作检验,全部是正品的概率为![]()
…………3分
至少有一件是次品的概率为![]() …………6分
…………6分
(2)设抽取n件产品作检验,则3件次品全部检验出的概率为![]() ………8分
………8分
由![]()
整理得:![]() ,……………………10分
,……………………10分
![]() ∴当n=9或n=10时上式成立.…………11分
∴当n=9或n=10时上式成立.…………11分
答:任意取出3件产品作检验,其中至少有1件是次品的概率为![]() 为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.………………12分
为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.………………12分
18、 (I) 设SC的中点为E,依题意:![]() 平面ABCD,又OE//SA,于是
平面ABCD,又OE//SA,于是![]() 平面ABCD则
平面ABCD则![]() 为OS与底面ABCD所成的角――――――――2分
为OS与底面ABCD所成的角――――――――2分
因为![]() 平面ABCD,所以
平面ABCD,所以![]() ,有
,有![]() ,所以
,所以![]() 平面SAC, 于是平面SAC
平面SAC, 于是平面SAC![]() 平面SBD. 因而点A在平面SBD上的射影点F必在OS上,即AF为
平面SBD. 因而点A在平面SBD上的射影点F必在OS上,即AF为![]() 的高且SF = 2OF于是
的高且SF = 2OF于是![]() ,
,![]() ,从而
,从而![]()
所以![]() ――――――4分
――――――4分
(II)过B作![]() ,连DG, 则
,连DG, 则![]() 为二面角B—SC—D的平面角, 设
为二面角B—SC—D的平面角, 设![]() ,则
,则![]() 从而
从而![]() ,
,![]() ,
,![]() ―――――6分
―――――6分
在![]() 中,
中,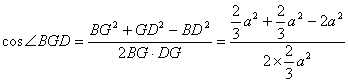
![]()
所以![]() .二面角B—SC—D的大小为
.二面角B—SC—D的大小为![]() ―――――8分
―――――8分
(III)设点C到平面SBD的距离为d由![]() 得
得
![]() ―――――――――――――10分
―――――――――――――10分
所以![]() ,故点C到平面SBD的距离为
,故点C到平面SBD的距离为![]() ――――――12分
――――――12分
19、(I)解法1: ![]() 的概率分布为
的概率分布为
|
| 1.2 | 1.18 | 1.17 |
| P |
|
|
|
E![]() =1.2
=1.2![]() +1.18
+1.18![]() +1.17
+1.17![]() =1.18.
=1.18.
由题设得![]() ,则
,则![]() 的概率分布为
的概率分布为
|
| 0 | 1 | 2 |
| P |
|
|
|
故![]() 的概率分布为
的概率分布为
|
| 1.3 | 1.25 | 0.2 |
| P |
|
|
|
所以![]() 的数学期望为
的数学期望为
E![]() =
=![]() +
+![]() +
+![]() =
=![]() .
.
解法2: ![]() 的概率分布为
的概率分布为
|
| 1.2 | 1.18 | 1.17 |
| P |
|
|
|
E![]() =1.2
=1.2![]() +1.18
+1.18![]() +1.17
+1.17![]() =1.18.
=1.18.
设![]() 表示事件”第i次调整,价格下降”(i=1,2),则
表示事件”第i次调整,价格下降”(i=1,2),则
P(![]() =0)=
=0)= ![]() ;
;
P(![]() =1)=
=1)=![]() ;
;
P(![]() =2)=
=2)=![]()
故![]() 的概率分布为
的概率分布为
|
| 1.3 | 1.25 | 0.2 |
| P |
|
|
|
所以![]() 的数学期望为
的数学期望为
E![]() =
=![]() +
+![]() +
+![]() =
=![]() .
.
(II) 由![]() ,得:
,得:
![]()
 因0<p<1,所以
因0<p<1,所以![]() 时,p的取值范围是0<p<0.3.
时,p的取值范围是0<p<0.3.
20、解:连接BD交AC于O,则BD⊥AC,
连接A1O
在△AA1O中,AA1=2,AO=1,
∠A1AO=60°
∴A1O2=AA12+AO2-2AA1·Aocos60°=3
∴AO2+A1O2=A12
∴A1O⊥AO,由于平面AA
平面ABCD,
所以A1O⊥底面ABCD
∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(0,-1,0),B(![]() ,0,0),C(0,1,0),
,0,0),C(0,1,0),
D(-![]() ,0,0),A1(0,0,
,0,0),A1(0,0,![]() )……………2分
)……………2分
(Ⅰ)由于![]() ,
,![]() ,
,
则![]()
∴BD⊥AA1……………………4分
(Ⅱ)由于OB⊥平面AA
∴平面AA![]()
设![]() ⊥平面AA1D
⊥平面AA1D
则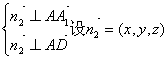
得到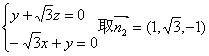 ……………………6分
……………………6分

所以二面角D—A![]() ……………8分
……………8分
(Ⅲ)假设在直线CC1上存在点P,使BP//平面DA
设![]()
则![]()
得![]() ……………………9分
……………………9分
设![]()
则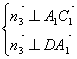 设
设![]()
得到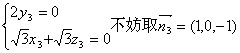 ……………………10分
……………………10分
又因为![]() 平面DA
平面DA
则![]() ·
·![]()
|
法二:在A1作A1O⊥AC于点O,由于平面AA
ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD

……………………4分
(Ⅱ)在△AA1O中,A
∠A1AO=60°∴AO=AA1·cos60°=1
所以O是AC的中点,由于底面ABCD为菱形,
所以O也是BD中点
由(Ⅰ)可知DO⊥平面AA
过O作OE⊥AA1于E点,连接OE,则AA1⊥DE
则∠DEO为二面角D—AA1—C的平面角
……………………6分
在菱形ABCD中,AB=2,∠ABC=60°
∴AC=AB=BC=2
∴AO=1,DO=![]()
在Rt△AEO中,OE=OA·sin∠EAO=![]()
DE=![]()
∴cos∠DEO=![]()
∴二面角D—A![]() ……………8分
……………8分
(Ⅲ)存在这样的点P
连接B![]() AB
AB![]() DC
DC
∴四边形A1B1CD为平行四边形.
∴A1D//B
在C
因B1B![]() CC1,……………………12分
CC1,……………………12分
∴BB1![]() CP, ∴四边形BB1CP为平行四边形
CP, ∴四边形BB1CP为平行四边形
则BP//B1C, ∴BP//A1D, ∴BP//平面DA
21.解:(Ⅰ)证法1:∵当![]()
即![]() 于是有
于是有 ![]()
所有不等式两边相加可得 ![]()
由已知不等式知,当n≥3时有,![]()
∵![]()
证法2:设![]() ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式
![]()
(i)当n=3 时, 由 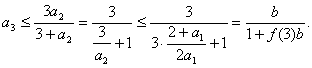
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即![]()
则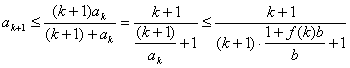
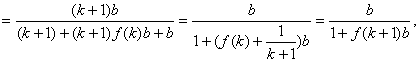
即当n=k+1时,不等式也成立.
由(i)、(ii)知,![]()
又由已知不等式得 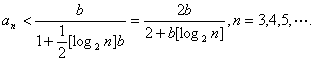
(Ⅱ)有极限,且![]()
(Ⅲ)∵![]()
则有![]()
故取N=1024,可使当n>N时,都有![]()


