高二理科数学下期末测试卷
命题人:林永忠 审核人:林伟
一、选择题(60分)
1、已知复数![]() ,则
,则![]() ( )
( )
A、 2 B、-2 C、2i D、 -2i
2、已知数列![]() ,那么“对任意的
,那么“对任意的![]() ,点
,点![]() 都在直线
都在直线![]() 上”是“
上”是“![]() 为等差数列”的 ( )
为等差数列”的 ( )
A、 充分而不必要条件 B、必要而不充分条件
C、 充要条件
D、既不充分也不必要条件![]()
3、椭圆![]() 的焦点为F1和F2,点P在椭圆上,如果线段PF1中点在y轴上,那么PF1是PF2的
( )
的焦点为F1和F2,点P在椭圆上,如果线段PF1中点在y轴上,那么PF1是PF2的
( )
A、7倍 B、5倍 C、4倍 D、3倍
4、已知平面![]() 与平面
与平面![]() 相交,直线
相交,直线![]() ,则
(
)
,则
(
)
A、![]() 内必存在直线与
内必存在直线与![]() 平行,且存在直线与
平行,且存在直线与![]() 垂直
垂直
B、![]() 内不一定存在直线与
内不一定存在直线与![]() 平行,不一定存在直线与
平行,不一定存在直线与![]() 垂直
垂直
C、![]() 内不一定存在直线与
内不一定存在直线与![]() 平行,但必存在直线与
平行,但必存在直线与![]() 垂直
垂直
D、![]() 内必存在直线与
内必存在直线与![]() 平行,却不一定存在直线与
平行,却不一定存在直线与![]() 垂直
垂直
5、甲、乙两人独立地解同一问题,甲解决这个问题的概率是![]() ,乙解决这个问题的概率是
,乙解决这个问题的概率是![]() ,那么恰好有1人解决这个问题的概率是
( )
,那么恰好有1人解决这个问题的概率是
( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、函数![]() ,已知
,已知![]() 在
在![]() 时取得极值,则
时取得极值,则![]() = ( )
= ( )
A、2 B、3 C、4 D、5
7、平行六面体![]() 中,
中,![]() 为
为![]() 与
与![]() 的交点。若
的交点。若![]() ,
,![]() ,
,![]() , 则下列向量中与
, 则下列向量中与![]() 相等的向量是
( )
相等的向量是
( )
A、![]() B、
B、 ![]() C、
C、 ![]() D、
D、 ![]()
8、已知定点A、B且AB=4,动点P满足PA-PB=3,则PA的最小值是( )
 A、
A、![]() B、
B、![]() C、
C、![]() D、5
D、5
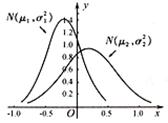
9、设两个正态分布![]() 和
和![]()
的密度函数图像如图所示。则有 ( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
10、有七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙、丙两倍同学要站在一起,则不同的站法有 ( )
 A、240种 B、192种
C、96种 D、48种
A、240种 B、192种
C、96种 D、48种
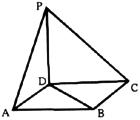
11、如图,点P在正方形ABCD所在的平面外,
![]() ,则PA与BD
,则PA与BD
所成角的度数为 ( )
A、30° B、45° C、60° D、90°
12、已知函数![]() ,
,![]() [-2,2]表示的
[-2,2]表示的
曲线过原点,且在x=±1处的切线斜率均为-1,有以下命题:
① f(x)的解析式为:![]() ,
,![]() [-2,2];
[-2,2];
② f(x)的极值点有且仅有一个;
③ f(x)的最大值与最小值之和等于零;
其中正确的命题个数为 ( )
A、0个 B、1个 C、2个 D、3个
二、填空题(16分)
13.抛物线![]() 的准线方程为 .
的准线方程为 .
14、在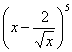 的二项展开式中,
的二项展开式中,![]() 的系数是 (用数字作答)
的系数是 (用数字作答)
15、某同学在电脑中打出如下若干个圈:
●○●○○●○○○●○○○○●○○○○○●……若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前2008个圈中的●的个数是 .
16、函数![]() 在区间
在区间![]() 上单调递增,那么实数a的取值范围是 。
上单调递增,那么实数a的取值范围是 。
三、解答题(74分)
17、已知命题p:关于![]() 的不等式
的不等式 ![]() ;
;
命题q:关于![]() 的方程
的方程![]() 有两个负根;
有两个负根;
求实数a的取值范围,使“p或q”为真命题,“p且q”为假命题.
18、投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,经过多次试验,某生投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋。
(1)记“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记
为事件A,B,C,求![]() ;
;
(2)求该人在4次投掷中恰有三次投入红袋的概率。
(3)求该人两次投掷后得分![]() 的数学期望。
的数学期望。
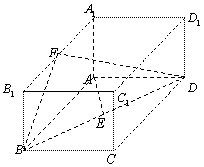 19、如图,已知长方体
19、如图,已知长方体![]()
![]() 直线
直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]() 垂直
垂直![]() 于
于![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求平面![]() 与平面
与平面![]() 所成的
所成的
锐二面角的余弦值;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
20、已知函数![]() ,
,
(1)求函数![]() 的导数;
的导数;
(2)设曲线![]() 在点(1,f(1))处的切线为
在点(1,f(1))处的切线为![]() ,若
,若![]() 与圆
与圆![]() 相切,求a的值;
相切,求a的值;
(3)若函数![]() 在
在![]() 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
21、已知![]() 定义在区间
定义在区间![]() 上, 且
上, 且![]() ,
,
设![]() 且
且![]() .
.
(1)求![]() 的值;
的值;
(2)求证:
![]()
(3)若![]() , 求证:
, 求证: ![]() .
.
22、已知焦点在![]() 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线![]() 对称.
对称.
(1)求双曲线C的方程;
(2)设直线![]() 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线![]() 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线![]() 在
在![]() 轴上的截距b的取值范围.
轴上的截距b的取值范围.
参考答案
1——12:AAACB;DACAB;CC。13、![]() ;14、40;15、62;16、
;14、40;15、62;16、![]() 。
。
17、解:对命题![]() :,由
:,由![]() ,解得:
,解得:![]() ; …………2分
; …………2分
对命题![]() :由
:由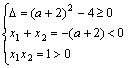 ,解得
,解得![]() . …………4分
. …………4分
要使p真q假,则![]() ;
…………7分
;
…………7分
要使p假q真,则 ,
…………10分
,
…………10分
综上所述,当![]() 的范围是
的范围是![]() 。 ………………12分
。 ………………12分
18解:(1)、“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记
为事件A,B,C。
则由题意知:![]() …………3分
…………3分
(2)因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为;![]() …………6分
…………6分
(3)两次投掷得分![]() 的得分可取值为0,1,2,3,4则:
的得分可取值为0,1,2,3,4则:
![]() ;
;![]()
![]() ;
;![]() ;
;
![]() ;
………………10分
;
………………10分
![]() …………12分
…………12分
19解:在长方体![]() 中,以
中,以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴建立如图示空间直角坐标系
轴建立如图示空间直角坐标系
由已知![]() 可得
可得![]() ,
,![]()
又![]() 平面
平面![]() ,从而
,从而![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,又
,又![]() ,
,![]() ,
,![]() 从而易得
从而易得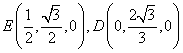
(1)易知平面![]() 的一个法向量
的一个法向量![]() 设
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]() , 由
, 由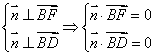
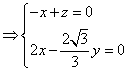
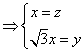 即
即![]() 所以
所以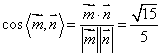 即平面
即平面![]() 与平面
与平面![]() 所成的二面角的大小(锐角)为
所成的二面角的大小(锐角)为![]() 。 …………6分
。 …………6分
(2)点![]() 到平面
到平面![]() 的距离,即
的距离,即![]() 在平面
在平面![]() 的法向量
的法向量![]() 上的投影的绝对值,所以距离
上的投影的绝对值,所以距离![]() =
=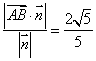 ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
………………12分
。
………………12分
20解:(1)![]() ………………2分
………………2分
(2)依题意有,![]() , 过
, 过![]() 点的直线的斜率为
点的直线的斜率为![]() ,
,
所以,过![]() 点的直线方程为
点的直线方程为![]()
又已知圆圆心为(-1,0)半径为1,
依题意![]() ,解之得
,解之得![]() . ………………7分
. ………………7分
(3)![]() 在
在![]() 上恒成立,
上恒成立,
![]() ,
,![]() ,故
,故![]() 。
………………12分
。
………………12分
21解: (1)由![]() 得
得![]() =-1 ………………2分
=-1 ………………2分
(2)∵![]() ,
, ![]()
∴![]()
∵![]() ∴
∴![]()
∵![]() ,
,![]() ∴
∴![]()
∴![]() ∴
∴![]() ;
;
即![]() ………………7分
………………7分
另解:![]() ,则
,则![]() 。
。
因为直线AB是曲线的一条割线,所以必存在一条切线与割线平行。
(3) ∵![]() 且
且![]() ……①
……①
又![]() =
=![]()
![]()
![]()
![]()
![]() ……②
……②
①+②得: ![]() , ∴
, ∴![]() ………………12分
………………12分
另解:![]()
22解:(1)设双曲线C的渐近线方程为y=kx,则kx-y=0∵该直线与圆![]() 相切,∴双曲线C的两条渐近线方程为y=±x.故设双曲线C的方程为
相切,∴双曲线C的两条渐近线方程为y=±x.故设双曲线C的方程为![]() .又双曲线C的一个焦点为
.又双曲线C的一个焦点为![]() ,∴
,∴![]() ,
,![]() .
.
∴双曲线C的方程为:![]() .
………………5分
.
………………5分
(2)由![]() 得
得![]() .令
.令![]()
∵直线与双曲线左支交于两点,
等价于方程f(x)=0在![]() 上有两个不等实根. ………………6分
上有两个不等实根. ………………6分
因此![]() ,解得
,解得![]() . ………………8分
. ………………8分
又AB中点为![]() ,
,
∴直线l的方程为:![]() . ……………… 10分
. ……………… 10分
令x=0,得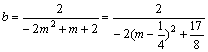 . ………………12分
. ………………12分
∵![]() ,∴
,∴![]() ,
,
∴![]() . ……………………14分
. ……………………14分