高一数学必修4练习题(四)
适用范围:第三章 《三角变换》
A组题(共100分)
一.选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.![]() 的值为( )
的值为( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
2. ![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C. -
C. -![]() D. -
D. -![]()
3. 函数![]() 的最小正周期为( )
的最小正周期为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 已知![]() 、
、![]() 都是锐角,
都是锐角,![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
5. 函数![]() 的最大值和最小值分别为( )
的最大值和最小值分别为( )
A. 最大值为1,最小值为-1 B. 最大值为2,最小值为-2
C. 最大值为![]() ,最小值为
,最小值为![]() D. 最大值为
D. 最大值为![]() ,最小值为-1
,最小值为-1
二.填空题:本大题共4小题,每小题6分,共24分。
6.已知![]() ,则
,则![]() =_______________。
=_______________。
7. 已知![]() ,则
,则![]() 的值为___________。
的值为___________。
8. ![]() =___________。
=___________。
9. 化简![]() =_______________。
=_______________。
三.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
10.(本小题13分)
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)证明:![]() .
.
11.(本小题14分)
已知A、B、C是![]() 的三内角,向量
的三内角,向量![]() ,
,![]() ,且
,且![]() .
.
(1)求角A;
(2)若![]() ,求
,求![]() .
.
12.(本小题14分)
已知![]() ,
,![]() 对
对![]() 恒成立,求满足条件
恒成立,求满足条件![]() 的范围.
的范围.
B组题(共100分)
四.选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
13.函数![]() 的单调递增区间是( )
的单调递增区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14. 已知函数![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
A.此函数的最小周期为![]() ,其图像的一个对称中心是
,其图像的一个对称中心是![]()
B.此函数的最小周期为![]() ,其图像的一个对称中心是
,其图像的一个对称中心是![]()
C.此函数的最小周期为![]() ,其图像的一个对称中心是
,其图像的一个对称中心是![]()
D.此函数的最小周期为![]() ,其图像的一个对称中心是
,其图像的一个对称中心是![]()
15. 若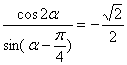 ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16. 已知锐角![]() 、
、![]() 满足
满足![]() ,则
,则![]() 为( )
为( )
A. ![]() B.
B.![]() C.
C. ![]() 或
或![]() D.
D.![]()
17. 函数![]() 在区间
在区间![]() 的简图是( )
的简图是( )
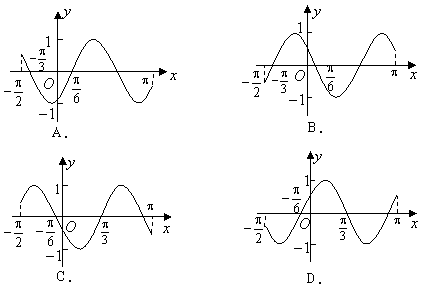
五.填空题:本大题共4小题,每小题6分,共24分。
 18.若
18.若![]() ,则
,则![]() 的取值范围是_______________;
的取值范围是_______________;
19. ![]() =________________;
=________________;
20. 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,那么
,那么![]() 的值等于 _____.
的值等于 _____.
21. 已知![]() ,则
,则![]() =________.
=________.
六.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
22.(本小题13分)
已知![]() ,
,![]() 为
为![]() 的最小正周期,
的最小正周期,![]() ,
,![]() ,且
,且![]() .求
.求![]() 的值.
的值.
23.(本小题14分)
已知函数 .
.
(1)求![]() 的定义域;
的定义域;
(2)若角![]() 在第一象限且
在第一象限且![]() ,求
,求![]() 的值.
的值.
24.(本小题14分)
已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,设
,设![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求函数![]() 的最大值与最小值.
的最大值与最小值.
C组题(共50分)
七.选择或填空题:本大题共2题。
25.已知函数![]() (
(![]() 、
、![]() 为常数,
为常数,![]() ,
,![]() )在
)在![]() 处取得最小值,则函数
处取得最小值,则函数![]() 是( )
是( )
A.偶函数且它的图象关于点![]() 对称 B.偶函数且它的图象关于点
对称 B.偶函数且它的图象关于点![]() 对称
对称
C.奇函数且它的图象关于点![]() 对称 D.奇函数且它的图象关于点
对称 D.奇函数且它的图象关于点![]() 对称
对称
26. 已知向量![]() ,则
,则![]() 的最大值为________;解答题:本大题共3小题,解答题应写出文字说明、证明过程或演算步骤。
的最大值为________;解答题:本大题共3小题,解答题应写出文字说明、证明过程或演算步骤。
27.设函数![]() (其中
(其中![]() >0,
>0,![]() ),且
),且![]() 的图象在y轴右侧的第一个高点的横坐标为
的图象在y轴右侧的第一个高点的横坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)如果![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求a的值.
,求a的值.
28.已知向量![]() 和
和![]() ,且
,且![]() 求
求![]() 的值.
的值.
29.已知![]() ,且
,且![]() .
.
求:
 的最大值,并求出相应的
的最大值,并求出相应的![]() 的值.
的值.
厦门市2007—2008学年数学必修4练习(四)参考答案
适用范围:第三章 《三角变换》
A组题(共100分)
一. 选择题: DCBAB
二. 填空题: 6.![]() 7.
7. ![]() 8.
1 9.
8.
1 9. ![]()
三. 解答题:
10.(本小题13分)
(1)解:∵![]() ,
,
![]() ,
,
两式相加得![]() ,……①
,……①
两式相减得![]() ,……②
,……②
②÷①得![]() =
=![]() .
.
(2)证明:![]()
=![]()
=![]() =
=![]() .
.
11.解:(1)∵![]() ∴
∴![]() ,即
,即![]()
![]() ,
, ![]()
∵![]() ,
,![]() ,∴
,∴![]() ,即
,即![]()
(2)由题知![]() ,整理得
,整理得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() 或
或![]()
而![]() 使
使![]() ,舍去,
,舍去,
∴![]() ,
,
∴![]()
=![]()
12.解:![]()
=![]() ,
,
令![]() ;
;
依题意 ![]() 对
对![]() 恒成立,
恒成立,
![]() ,得
,得![]() ;
;
![]() 满足条件
满足条件![]() 的范围为
的范围为![]() .
.
B组题(共100分)
四. 选择题: DBCAA
五. 填空题:18. ![]() 19.
19. ![]() 20.
20. ![]() 21. 2
21. 2
六. 解答题:
22.解:因为![]() 为
为![]() 的最小正周期,故
的最小正周期,故![]() .
.
因![]() ,又
,又![]() .
.
故![]() .
.
由于![]() ,所以
,所以![]() =
=![]()
=![]()
=![]() =
=![]()
23.解:(1)由![]() ,得
,得![]() ,
,![]() ;
;
故![]() 的定义域为
的定义域为![]()
(2)由已知条件得![]() ;
;
从而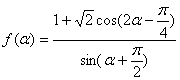 =
=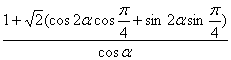
=![]() =
=![]()
 =
=![]()
24.解:(1)设![]() 中角
中角![]() 的对边分别为
的对边分别为![]() ,
,
∵![]() 的面积为
的面积为![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
可得![]() ,∴
,∴![]() .
.
(2)![]() =
=![]()
=![]() =
=![]() .
.
![]() ,
,
∴当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() .
.
C组题(共50分)
七. 选择或填空题:25 D 26. ![]()
八. 解答题:
27.解:(1)![]()
=![]()
=![]() ,
,
∵![]() 的图象在y轴右侧的第一个高点的横坐标为
的图象在y轴右侧的第一个高点的横坐标为![]() ,
,
![]() ,
,![]() ;
;
(2)由(1)的![]() ,
,
![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 取最小值
取最小值![]() ,
,
∴![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,
,
![]() ,
,![]()
28.解法一:![]()
![]()
=![]() =
=![]() ,
,
由已知![]() ,得
,得![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
![]() 。
。
解法二:![]()
=![]()
=![]()
=![]() ,
,
∵![]() ,
, ![]()
![]() ,
,![]() ,
,![]() ,
,
![]() 。
。
29.解:
= =
=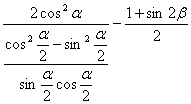
=![]() =
=![]()
=![]()
=![]()
![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
![]() ;
;
当![]() 时,y取最大值
时,y取最大值![]() ,
,
这时 ,得
,得![]() ;
;
即当![]() 时,
时,![]() .
.